8.2.1. Задание: Построить перпендикуляр из точки А на плоскость 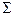 (
(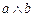 ) и найти точку пересечения перпендикуляра с плоскостью.
) и найти точку пересечения перпендикуляра с плоскостью.
Решение: исходя из принципа перпендикулярности прямой и плоскости (прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости), необходимо в плоскости провести две пересекающиеся прямые: горизонталь h и фронталь f (рис. 8.9).

Рис.8.9
Затем из точки
А проводим нормаль
n к плоскости
Σ. На основании теоремы о проецировании прямого угла
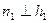
и
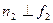
. Если плоскость задана следами, то
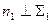
и
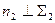
(рис. 8.10).
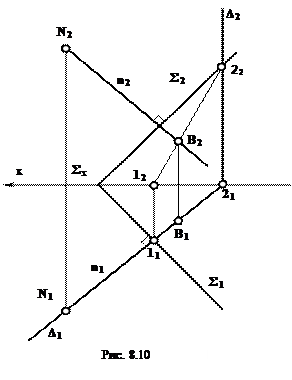
Основание перпендикуляра определяется как точка пересечения его с плоскостью. Для этого нужно провести через нормаль проецирующую плоскость 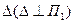 , найти линию пересечения l(l1,l2)-2(21,22)плоскостей Σ и
, найти линию пересечения l(l1,l2)-2(21,22)плоскостей Σ и 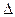 и на пересечении проекции этой линии с проекцией нормали отметить общую точку В для нормали и плоскости.
и на пересечении проекции этой линии с проекцией нормали отметить общую точку В для нормали и плоскости.
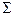 (
(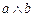 ) и найти точку пересечения перпендикуляра с плоскостью.
) и найти точку пересечения перпендикуляра с плоскостью.
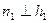 и
и 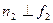 . Если плоскость задана следами, то
. Если плоскость задана следами, то 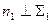 и
и 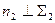 (рис. 8.10).
(рис. 8.10).

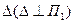 , найти линию пересечения l(l1,l2)-2(21,22)плоскостей Σ и
, найти линию пересечения l(l1,l2)-2(21,22)плоскостей Σ и 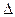 и на пересечении проекции этой линии с проекцией нормали отметить общую точку В для нормали и плоскости.
и на пересечении проекции этой линии с проекцией нормали отметить общую точку В для нормали и плоскости. 2014-02-24
2014-02-24 2090
2090
