2014-02-09
687
Теорема. Если вероятность наступления события 
в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие произойдёт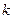 
раз в 
испытаниях при достаточно большом числе приблизительно равна
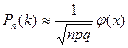- формула Лапласа,
где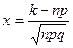 
, 
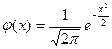- функция Гаусса.
Формула Лапласа даёт незначительную погрешность, если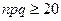 
.
Для упрощения расчётов составлена таблица значений функции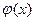 
, которая приводится в приложениях учебников.
Свойста функци 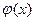, ее график
1) Чётная: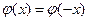 
, т.е. график симметричен относительно оси 
.
2) С осью пересекается в точке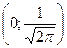 
.
3) С осью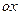 
не пересекается, так как при любых значениях 
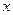показательная функция 
.
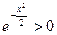4) Ось 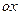является горизонтальной асимптотой, так как 
.
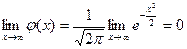Следовательно,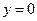 
- горизонтальная асимптота.
5) Исследуем функцию на экстремум. Найдем первую производную и определим критические точки:
, 
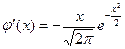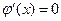. Т.о. 
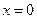- критическая точка.
Т.к. на интервале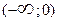 
функция возрастает, а на интервале 
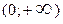- убывает, то
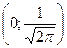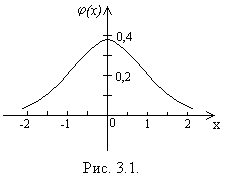
точка - точка максимума. График функции 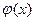построен на рис. 3.1.
