2014-02-09
959
Пусть производится несколько испытаний. В каждом из этих испытаний вероятность появления события 
не зависит от исходов других испытаний и является величиной постоянной равной р. Следовательно, вероятность ненаступления события в каждом испытании также постоянна и равна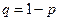 
.
Поставим перед собой задачу вычислить вероятность того, что в 
испытаниях событие произойдёт ровно 
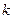раз.
Теорема. Если вероятность наступления события в каждом испытании постоянна, то вероятность того, что в испытаниях событие появится ровно 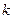раз равна
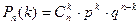- формула Бернулли.
Доказательство.Предположим, что событие появилось 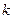раз по порядку, а затем 
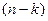раз не появилось. Найдем вероятность события 
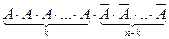по теореме умножения вероятностей независимых событий
.
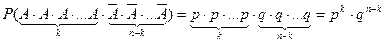Число всех комбинаций будет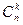 
и вероятность каждой такой комбинации равна 
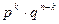. Т.к. все комбинации между собой несовместны, то по теореме сложения вероятностей несовместных событий имеем 
.
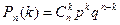Пример 3.1. Два равносильных игрока играют в шахматы. Что вероятнее выиграть 1 раз из 2-х партий или 2 раза из 4-х?
|
|
|
Решение. Найдем вероятности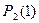 
, 
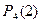по формуле Бернулли.
Вероятность выигрыша в одной партии равна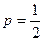 
, следовательно, 
.
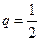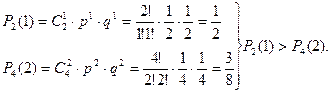
Вероятнее выиграть одну партию из двух.
