Тема 2. Основные теоремы
Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий
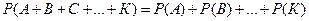 .
.
В частности 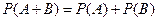 .
.
Доказательство рассмотрим на примере суммы 2-х событий  и
и 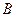 .
.
Пусть  - общее число возможных исходов некоторого испытания;
- общее число возможных исходов некоторого испытания; 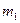 - число исходов, благоприятствующих событию
- число исходов, благоприятствующих событию  ;
; 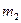 - число исходов, благоприятствующих событию
- число исходов, благоприятствующих событию 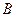 . Тогда
. Тогда 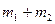 - число исходов, благоприятствующих наступлению либо события
- число исходов, благоприятствующих наступлению либо события  , либо события
, либо события 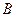 , т.е. события
, т.е. события 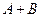 .
.
Следовательно, 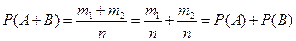 .
.
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.
Если А, В,…, К образуют полную группу, то 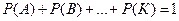 .
.
Следствие 2. Сумма вероятностей противоположных событий равна единице
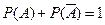 или
или 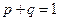 .
.
Пример 2.1. В ящике 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность появления цветного шара.
Решение. Пусть событие С = {появление цветного шара}. Появление цветного шара означает появление либо красного шара (событие ), либо синего шара (событие
), либо синего шара (событие 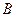 ).
). 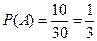 ,
, 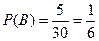 . Т.к. события
. Т.к. события  и
и 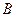 несовместные, то
несовместные, то
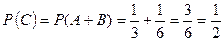 .
.
Пример 2.2. Вероятность того, что день будет пасмурным равна 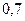 . Найти вероятность того, что день будет ясным.
. Найти вероятность того, что день будет ясным.
Решение. События день дождливый ( ) и день ясный (
) и день ясный (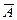 ) – противоположные. Следовательно,
) – противоположные. Следовательно, 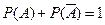 ,
, 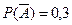 .
.
 2014-02-09
2014-02-09 563
563








