Определение. Условной вероятностью события 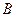 называют вероятность события
называют вероятность события 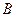 , вычисленную в предположении, что событие
, вычисленную в предположении, что событие  уже наступило.
уже наступило.
Обозначают 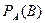 или
или 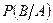 .
.
Пример 2.3. В ящике 5 деталей: 3 стандартные и 2 бракованные. Дважды из него извлекается по одной детали без возврата. Найти условные вероятности извлечения во второй раз стандартной детали.
Решение. Обозначим через событие 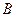 = {извлечение стандартной детали во второй раз}.
= {извлечение стандартной детали во второй раз}. 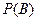 зависит от того, какую деталь вытащили в первый раз. Пусть событие
зависит от того, какую деталь вытащили в первый раз. Пусть событие  = {в первый раз извлекли стандартную деталь}, событие
= {в первый раз извлекли стандартную деталь}, событие 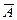 = {в первый раз извлекли бракованную деталь}. Тогда условные вероятности равны
= {в первый раз извлекли бракованную деталь}. Тогда условные вероятности равны
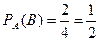 ,
, 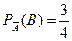 .
.
Теорема умножения вероятностей. Вероятность произведения событий  и
и 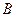 равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло
равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло
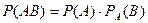 или
или 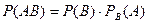 .
.
Доказательство. Пусть количество исходов некоторого испытания равно  . Из них событию
. Из них событию  благоприятствует
благоприятствует 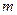 случаев, из которых событию
случаев, из которых событию 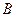 благоприятствует
благоприятствует 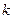 случаев. Отсюда
случаев. Отсюда 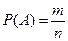 ,
, 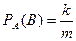 .
.
Произведению событий 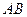 благоприятствуют
благоприятствуют 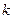 случаев. Найдем вероятность этого события
случаев. Найдем вероятность этого события
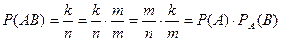 .
.
Пример 2.4. Среди 25 электролампочек 4 нестандартные. Найти вероятность того, что взятые 2 лампочки окажутся нестандартными.
Решение. 1 способ. Пусть событие А = {взяты две нестандартные лампочки}. Выбрать 2 лампочки из имеющихся 25 можно 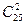 способами, а 2 нестандартные лампочки из 4 имеющихся
способами, а 2 нестандартные лампочки из 4 имеющихся 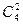 способами. Отсюда
способами. Отсюда 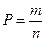 ;
; 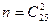 ;
; 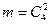 .
.
Т.о. 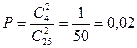 .
.
2 способ. Пусть событие = {первая взятая лампочка нестандартная}, событие
= {первая взятая лампочка нестандартная}, событие 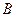 = {вторая взятая лампочка нестандартная}. Найдем вероятности этих событий:
= {вторая взятая лампочка нестандартная}. Найдем вероятности этих событий:
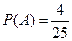 ,
, 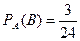 . Согласно теореме умножения
. Согласно теореме умножения 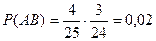 .
.
Теорема умножения принимает более простой вид, когда события, образующие произведение, независимы.
Определение. Событие 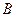 называется независимым от события
называется независимым от события  , если его вероятность не меняется от того, произошло событие
, если его вероятность не меняется от того, произошло событие  или нет, т.е.
или нет, т.е. 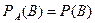 .
.
В противном случае события  и
и 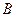 называются зависимыми.
называются зависимыми.
Теорема умножения вероятностей для независимых событий имеет вид
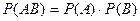 .
.
Пример 2.5. Вероятность попадания в цель для I-го стрелка равна 0,8, для II-го – 0,7, для III-го – 0,9. Каждый из стрелков делает по одному выстрелу. Найти вероятность того, что в мишени 3 попадания.
Решение. Обозначим через события А 1 = {первый стрелок попал}, А 2 = {второй стрелок попал}, А 3 = {третий стрелок попал}. Т.к. события А 1, А 2, А 3 независимые, то можно использовать теорему умножения вероятностей для независимых событий
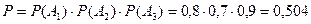 .
.
 2014-02-09
2014-02-09 2246
2246
