2014-02-09
1499
1) Вероятность попадания нормально распределенной случайной величины 
в интервал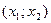 
равна
.
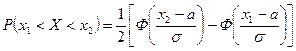2) Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания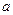 
не превысит по абсолютному значению величину 
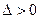, равна:
.
Из этого свойства следует «правило трёх сигм».
Рассмотрим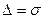 
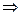
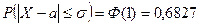
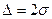
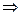
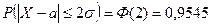
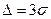
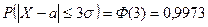
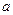Правило. Таким образом, если случайная величина имеет нормальный закон распределения с параметрами и 
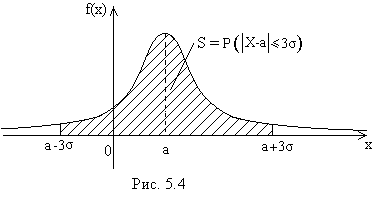
, то практически достоверно, что её значения заключены в интервале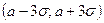 
(рис. 5.4).
