2014-02-09
848
1) 
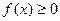(свойство неотрицательности);
2)
(свойство нормированности);
В частности, если все значения случайной величины принадлежат интервалу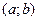 
, то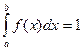 
.
Пример 5.2. Плотность распределения 
случайной величины 
задана функцией 
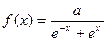. Найти параметр 
.
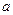Решение. должна удовлетворять свойству нормированности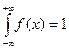 
. Найдем несобственный интеграл
Следовательно,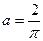 
.
Таким образом, из свойств плотности вероятности следует, что её график лежит не ниже оси абсцисс и площадь фигуры, ограниченной кривой распределения и осью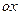 
, равна единице.
