Определение. Математическим ожиданием непрерывной случайной величины  , возможные значения которой принадлежат интервалу
, возможные значения которой принадлежат интервалу 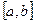 , называют определённый интеграл
, называют определённый интеграл  .
.
Если возможные значения с.в. Х принадлежат всей оси 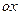 , то
, то 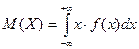 .
.
По аналогии с дисперсией дискретной случайной величины определяется дисперсия непрерывной случайной величины.
Определение. Если возможные значения с.в.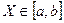 , то
, то
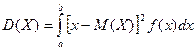 .
.
Если значения с.в. принадлежат всей оси
принадлежат всей оси 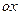 , то
, то 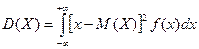 . Формула для расчёта дисперсии имеет вид:
. Формула для расчёта дисперсии имеет вид:

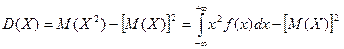 .
.
Все свойства 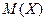 и
и 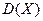 , рассмотренные для дискретных случайных величин, справедливы и для непрерывных случайных величин.
, рассмотренные для дискретных случайных величин, справедливы и для непрерывных случайных величин.
Среднеквадратическое отклонение 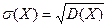 .
.
Пример 5.3. Непрерывная случайная величина задана в виде 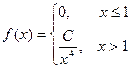 Найти значение
Найти значение 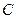 ,
, 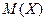 ,
, 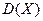 ,
, 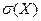 .
.
Решение. По свойству нормированности  . Найдем значение параметра С, решив несобственный интеграл
. Найдем значение параметра С, решив несобственный интеграл 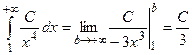 , т.е.
, т.е.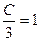 , отсюда
, отсюда 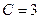 .
.
Математическое ожидание найдем по формуле  . Получаем
. Получаем
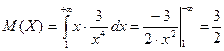 .
.
Дисперсия равна

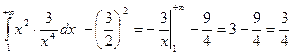 .
.
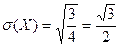 .
.
 2014-02-09
2014-02-09 410
410








