Определение. Условным законом распределения одной из случайной величины, входящих в систему 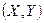 , называется закон её распределения, найденный при условии, что другая случайная величина приняла определённое значение (или попала в некий интервал).
, называется закон её распределения, найденный при условии, что другая случайная величина приняла определённое значение (или попала в некий интервал).
В случае двух дискретных случайных величин 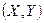 условным законом распределения случайной величины
условным законом распределения случайной величины  при условии
при условии 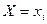 называется вероятность
называется вероятность
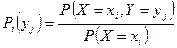 .
.
Аналогично определяется условный закон распределения дискретной случайной величины  при условии
при условии 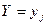 :
:
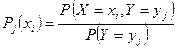 .
.
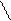 X Y X Y
| |||
| 0,1 | 0,2 | 0,15 | |
| 0,3 | 0,1 | 0,15 |
Пример 6.1. Закон распределения дискретной двумерной случайной величины задан таблицей
Найти: а) законы распределения случайных величин 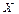 и
и  .
.
б) функцию распределения д.с.в. Х.
в) условный закон распределения с.в. Y при Х = 1.
г) вероятность события 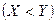 .
.
Решение.
а) Случайная величина Х принимает два значения: х 1 =1 и х 2 =2 с вероятностями
р 1 = 0,1 + 0,2 + 0,15 = 0,45 и р 2 = 0,3 + 0,1 + 0,15 = 0,55.
Случайная величина Y принимает три значения: у 1 =1, у 2 =2 и у 3 =3 с вероятностями р 1 = 0,1 + 0,3 = 0,4, р 2 = 0,2 + 0,1 = 0,3 и р 3 = 0,15 + 0,15 = 0,3.
| Х P | 0,45 | 0,55 |
| Y P | 0,4 | 0,3 | 0,3 |
Следовательно, законы распределения с.в. Х и Y можно представить в виде
б) В соответствии с формулой 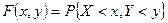 получаем:
получаем:
если 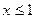
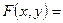 0;
0;
если 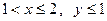
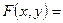 0;
0;
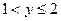
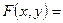 Р (Х =1, Y =1) = 0,1;
Р (Х =1, Y =1) = 0,1;
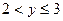
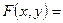 Р (Х =1, Y =1) + Р (Х =1, Y =2) = 0,1+ 0,2 = 0,3;
Р (Х =1, Y =1) + Р (Х =1, Y =2) = 0,1+ 0,2 = 0,3;
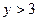
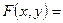 Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =1, Y =3) = 0,1+ 0,2 +
Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =1, Y =3) = 0,1+ 0,2 +
+ 0,15 = 0,45;
если 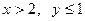
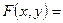 0;
0;
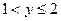
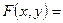 Р (Х =1, Y =1) + Р (Х =2, Y =1) = 0,1+ 0,3 = 0,4;
Р (Х =1, Y =1) + Р (Х =2, Y =1) = 0,1+ 0,3 = 0,4;
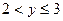
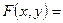 Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =2, Y =1) + Р (Х =2, Y =2) =
Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =2, Y =1) + Р (Х =2, Y =2) =
= 0,1+ 0,2+ 0,3+ 0,1 = 0,7;
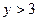
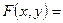 Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =1, Y =3) + Р (Х =2, Y =1) +
Р (Х =1, Y =1) + Р (Х =1, Y =2) + Р (Х =1, Y =3) + Р (Х =2, Y =1) +
+ Р (Х =2, Y =2) + Р (Х =2, Y =3) = 1.
Таким образом, функция распределения с.в. Х и Y имеет вид
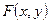
| 
| 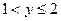
| 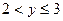
| 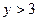
|
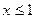
| ||||
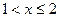
| 0,1 | 0,3 | 0,45 | |
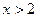
| 0,4 | 0,7 |
в) Условный закон распределения  при условии, что Х=1, получим, если вероятности значений
при условии, что Х=1, получим, если вероятности значений  найдем с помощью формулы
найдем с помощью формулы 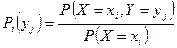 .
.
Так как 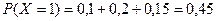 , то
, то
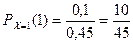 ,
, 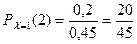 ,
, 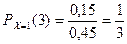 .
.
Таким образом, условный закон распределения с.в.  при Х=1 имеет вид
при Х=1 имеет вид
| Y | |||
| РХ=1 | 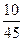
| 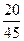
| 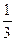
|
г) Для нахождения вероятности события 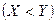 складываем вероятности событий для которых
складываем вероятности событий для которых 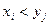 . Получим Р
. Получим Р 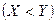 = 0,2 + 0,15 + 0,15 = 0,5.
= 0,2 + 0,15 + 0,15 = 0,5.
 2014-02-09
2014-02-09 441
441








