2014-02-09
902
Для характеристики связи между величинами 
и 
служат ковариация и коэффициент корреляции.
Определение. Ковариацией (или корреляционным моментом)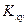 
случайных величин и называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, то есть
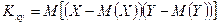
или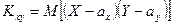 
,
где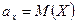 
, 
.
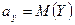Из определения следует, что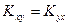 
.
Для дискретных случайных величин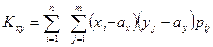 
.
Ковариацию удобно вычислять по формуле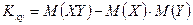 
.
Если случайные величины и независимы, то 
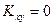. Таким образом, если 
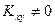, то случайные величины и зависимы, в этом случае случайные величины называют коррелированными. В случае 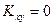случайные величины и называют некоррелированными.
Ковариация характеризует не только степень зависимости двух случайных величин, но и их разброс вокруг точки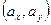 
. Она является величиной размерной, что затрудняет её использование для оценки степени зависимости для различных случайных величин. Этих недостатков лишён коэффициен корреляции.
Определение. Коэффициентом корреляции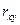 
двух случайных величин и называется безразмерная величина, равная
,
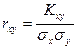где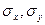 
- среднеквадратические отклонения соответственно величин и .
