Сильная сходимость последовательности операторов. Теорема Банаха – Штейнгауза

Определение 1.1. Пусть X и Y – линейные нормированные пространства. Последовательность операторов { A_n } Ì L (X, Y) сходится к оператору A сильно, если для любого x Î X последовательность { A_n x } сходится к A x.

Введение сильной сходимости последовательности операторов { A_n } мотивируется тем, что встречаются последовательности операторов, которые естественно считать сходящимися, но они оказываются не сходящимися по норме.

Пример 1.5. Пусть H – гильбертово пространство, { e_k } – ортонормированный базис в H. Любой элемент x Î H представляется в виде ряда Фурье 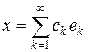. Построим оператор P_n, 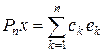. Этот оператор является проектором на подпространство L_n, порожденное элементами { e ₁, e ₂, ¼, e_n } (см. теорему 18.1 курса «Функциональный анализ. Часть 1»). Равенство 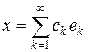по определению означает, что P_n x ® x, т. е. последовательность операторов сильно сходится к единичному оператору. Оператор I – P_n есть проектор на подпространство 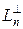и поэтому || I – P_n || = 1, т. е. P_n по норме не сходится к единичному оператору. Аналогичные примеры можно построить и в других пространствах.

Лемма 1.1. Если последовательность { A_n } Ì L (X, Y) сходится по норме к оператору A, то { A_n } сходится к A сильно.

Доказательство. Возьмем x Î X. Тогда || A_n x – A x || £ || A_n – A || || x || ® 0 при n ® ¥. Лемма доказана.

Как показано в примере, из сильной сходимости не вытекает сходимость по норме.

В определении предела сильно сходящейся последовательности операторов не требуется, чтобы предельный оператор был линейным ограниченным. Если A_n ® A сильно и A_n линейные, то, переходя к пределу в равенствах A_n (x ₁ + x ₂) = A_n x ₁ + A_n x ₂, A_n (l x) = l A_n x, убеждаемся, что оператор A линейный. Однако в неполных пространствах оператор A может не быть ограниченным.

Имеется аналогия между двумя типами сходимости в пространствах функций – равномерной и точечной – и двумя типами сходимости в пространстве линейных ограничейных операторов – равномерной и сильной. Отметим, что предел точечно сходящейся последовательности непрерывных функций может не быть непрерывной функцией. Аналогично и предел сильно сходящейся последовательности ограниченных (непрерывных) линейных операторов может не быть непрерывным.

Пример 1.6. На линейном пространстве C ¹[0, 1] зададим норму 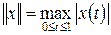. Рассмотрим оператор дифференцирования 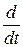как оператор из C ¹[0, 1] в C [0, 1]. Этот оператор неограничен (см пример 15.4 курса «Функциональный анализ. Часть 1»). Пусть разностный оператор A_n задан формулой

.

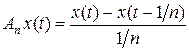Тогда для любого x Î C ¹[0, 1] последовательность { A_n x } равномерно сходится к 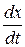, т. е. 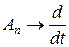сильно. Таким образом, последовательность ограниченных линейных операторов сильно сходится к неограниченному оператору 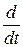. Если пространство, на котором определен оператор, полно, то такой пример невозможен. Это утверждение является одним из следствий следующей фундаментальной теоремы.

Теорема 1.1 (принцип равномерной ограниченности) (С.Банах, Г.Штейнгауз). Пусть X – банахово пространство, Y – нормированное пространство и пусть M – множество ограниченных линейных операторов M Ì L (X, Y) такое, что для любого x Î X существует постоянная C_x > 0 такая, что || A x || £ C_x для любого A Î M. Тогда M – ограниченное множество, т. е. существует постоянная C такая, что || A || £ C для любого A Î M.

Доказательство. Так как 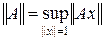, то условие || A || £ C эквивалентно тому, что || A x || £ C при || x || £ 1. Таким образом, нужно доказать, что множество чисел V £ {|| A x || : || x || £ 1, A Î M } ограничено, т. е. нормы || A x || ограничены в совокупности на единичном шаре. Покажем, что если нормы || A y || ограничены постоянной C ₀ на каком-нибудь шаре B [ y ₀, r ₀], r ₀ > 0, то || A x || ограничены на единичном шаре. Действительно, если || x || £ 1, то x = (1 / r ₀) (y – y ₀), где y Î B [ y ₀, r ₀]. Тогда || A x || £ (1 / r ₀) (|| A y || + || A y ₀ ||) £ (1 / r ₀) (C ₀ + C ₀) = C.

Предположим теперь, что множество V неограничено. Тогда по доказанному множество чисел || A x || не ограничено на каждом замкнутом шаре ненулевого радиуса и, в частности, не ограничено на каждом открытом шаре. Возьмем произвольный шар B [ x ₀, r ₀]. Так как на открытом шаре B (x ₀, r ₀) множество норм не ограничено в совокупности, то существует оператор A ₁ Î M и точка x ₁ Î B (x ₀, r ₀) такие, что || A ₁ x ₁ || > 1. В силу непрерывности оператора A ₁ существует шар B [ x ₁, r ₁] такой, что || A ₁ x || > 1 для всех x Î B [ x ₁, r ₁]. Для достаточно малого r ₁ (r ₁ < r ₀ – || x ₀ – x ₁ ||) имеем B [ x ₁, r ₁] Ì B [ x ₀, r ₀]. Выберем также r ₁ < r ₀ / 2. Далее, взяв шар B [ x ₁, r ₁], находим оператор A ₂ и шар B [ x ₂, r ₂] такие, что || A ₂ x || > 2 для всех x Î B [ x ₂, r ₂], причем B [ x ₂, r ₂] Ì B [ x ₁, r ₁], r ₂ < r ₀ / 2². Продолжая процесс, получаем последовательность B [ x_k, r_k ] замкнутых, вложенных друг в друга шаров, причем r_k ® 0, и последовательность операторов { A_k } такую, что для x Î B [ x_k, r_k ] имеем || A_k x || > k. Согласно принципу вложенных шаров (теорема 10.3 курса «Функциональный анализ. Часть 1»), существует точка x ^* Î B [ x_k, r_k ] для любого k. Тогда || A_k x ^* || > k и, значит, множество чисел || A_k x ^* || не ограничено в совокупности, что противоречит условию. Теорема доказана.

Замечание 1.1. || A x || можем рассматривать как функцию двух переменных A (A Î M) и x (|| x || £ 1). В теореме дана ограниченность этой функции по каждой из переменных (при фиксированном A || A x || £ || A || по определению ограниченности оператора, при фиксированном x – по условию теоремы). В теореме доказана ограниченность функции по совокупности переменных.

Простейший пример функции

f (х, y) = x y / (x + y), x > 0, y > 0

показывает, что для произвольных функций двух переменных такое утверждение не имеет места.

Следствие 1.1. Пусть X – банахово пространство, Y – нормированное. Если последовательность { A_n } Ì L (X, Y) сильно сходится к оператору A, то

1) последовательность { A_n } ограничена по норме,

2) оператор A ограничен.

Доказательство. Проверим, что множество { A_n } удовлетворяет условиям теоремы Банаха – Штейнгауза. Действительно, { A_n } – сходящаяся последовательность и, значит, || A_n x || £ C_x. По теореме Банаха – Штейнгауза || A_n || £ C. Тогда справедливо неравенство || A_n x || £ C || x ||. Переходя к пределу, получаем неравенство ограниченности для оператора A. Следствие доказано.

Определение 1.2. Последовательность { A_n } Ì L (X, Y) называется последовательностью Коши в смысле сильной сходимости, если для любого x Î X { A_n x } есть последовательность Коши в Y.

Следствие 1.2. Если X и Y – банаховы пространства, то пространство L (X, Y) полно в смысле сильной сходимости.

Доказательство. Пусть { A_n } – последовательность Коши в смысле сильной сходимости. Так как пространство Y полное, то A_n x ® y и мы получаем оператор A : x ® y. Этот оператор линейный и по следствию 1.1 ограниченный. По построению A_n ® A сильно. Следствие доказано.