Определение линейного функционала. Примеры линейных ограниченных функционалов. Теорема Рисса

Лекция 4 Линейные ограниченные функционалы. Теорема Хана – Банаха о продолжении линейного функционала

4.1. Определение линейного функционала. Примеры линейных ограниченных функционалов. Теорема Рисса

4.2. Теорема Хана – Банаха о продолжении линейного функционала и ее следствия

Определение 4.1. Линейным функционалом на линейном пространстве X над полем K называется отображение f : X ® K, удовлетворяющее условиям

f (x ₁ + x ₂) = f (x ₁) + f (x ₂), f (l x) = l f (x)

для любых x ₁, x ₂ Î X, l Î K.

Сопоставляя определение 4.1 с определениями лекции 15 курса «Функциональный анализ. Часть 1», видим, что линейный функционал является частным случаем линейного оператора. В частности, для линейного функционала справедливы все понятия и теоремы лекции 1.

Приведем некоторые из этих понятий.

1. Линейный функционал на нормированном пространстве X называется ограниченным, если существует постоянная C > 0 такая, что справедливо неравенство | f (x) | £ C || x ||.

2. Нормой ограниченного линейного функционала f называется наименьшая из констант C, при которых справедливо неравенство ограниченности, т. е. || f || = inf C =.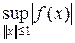

Определение 4.2. Пространство L (X, K) линейных ограниченных функционалов на X называется сопряженным к пространству X и обозначается X '.

Согласно теореме 1.1, сопряженное пространства является полным нормированным пространством.

Пример 4.1. Пусть X – конечномерное нормированное пространство с базисом e ₁, e ₂,¼, e_n. Тогда любой элемент x представляется в виде 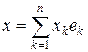, x_k Î R. Поскольку в X все нормы эквивалентны (см. раздел 16.1 курса «Функциональный анализ. Часть 1»), будем считать, что 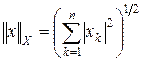. Если f – линейный функционал на X, то 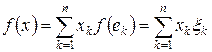, где x_k = f (e_k). Полагая 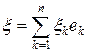, имеем f (x) = (x, x). Из неравенства Коши – Буняковского получаем оценку | f (x) | = | (x, x) | £ || x || || x ||, которая показывает, что в конечномерном нормированном пространстве любой линейный функционал f ограничен.

Пример 4.2. Пусть X = C [0, 1]. Функционал f на X определим формулой 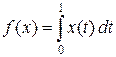. Линейность функционала f следует из свойств интеграла:

.

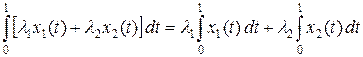Проверим ограниченность этого функционала:

.

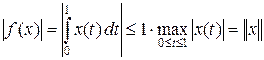Пример 4.3. Пусть a (t) – интегрируемая по Лебегу функция. На нормированном пространстве C [0, 1] определим функционал формулой 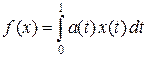, где интеграл понимается в смысле Лебега. Линейность этого функционала очевидна. Неравенство 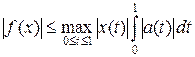есть неравенство ограниченности для функционала f, причем .

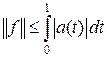На пространстве C [0, 1] могут быть функционалы и других видов.

Пример 4.4. На пространстве C [– 1, 1] определим линейный функционал d формулой d (x) = x (0). Так как | d (x) | = | x (0) | £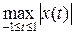, то функционал d ограничен и || d || = 1. Однако не существует функции a (t) Î L ₁ [– 1, 1] такой, что 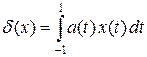для всех x Î C [– 1, 1]. Действительно, предположим противное и выберем последовательность

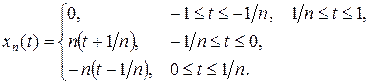
Тогда x_n Î C [– 1, 1] и x_n (0) = 1 для всех n. Подставляя x_n в формулу, получаем

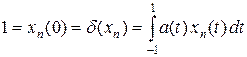. (1)

Так как a (t) x_n (t) ® 0 почти всюду и | a (t) x_n (t) | £ | a (t) |, то, переходя в равенстве (1) к пределу по теореме Лебега, будем иметь 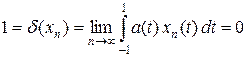. Получаем противоречие.

Пример 4.5. Пусть X = L_p (T, m) и пусть g Î L_q (T, m), где 1 / p + 1 / q = 1. На пространстве L_p (T, m) определим линейный функционал формулой

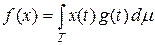. (2)

Согласно неравенству Гёльдера (см. раздел 11.2 курса «Функциональный анализ. Часть 1»), интеграл (2) существует и справедливо неравенство

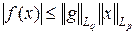, (3)

которое является неравенством ограниченности для функционала f, и из (3) получаем, что .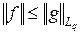

Пример 4.6. Пусть H – гильбертово пространство и u Î H – произвольиый элемент H. Линейный функционал на H определим формулой f (x) = (x, u). Линейность этого функционала следует из аксиом скалярного произведения, а неравенство Коши – Буняковского | (x, u) | £ || x || || u || является неравенством ограниченности для функционала f и показывает, что || f || £ || u ||. Так как в случае x = u имеем равенство f (u) = (u, u) = || u || || u ||, то постоянная || u || есть наименьшая, при которой справедливо неравенство ограниченности, т. е. || f || = || u ||.

Следующая теорема утверждает, что справедливо и обратное.

Теорема 4.1 (Рисс). Для любого ограниченного функционала f на гильбертовом пространстве H существует, и притом единственный, элемент u Î H такой, что f (x) = (x, u), причем || f || = || u ||.

Доказательство. Единственность. Пусть f (x) = (x, u ₁) и f (x) = (x, u ₂). Тогда (x, u ₁ – u ₂) = 0 для любого x Î H. Положив x = u ₁ – u ₂, имеем || u ₁ – u ₂||² = 0, т. е. u ₁ = u ₂.

Существование. Пусть N = Ker f = { x : x Î H, f (x) = 0}. Это линейное подпространство в H. Оно замкнуто в силу непрерывности f. (Если x_n ® x ₀ и x_n Î N, то 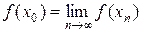, т. e. x ₀ Î N.) Если N = H, то f (x) = (x, 0). Пусть N ¹ H, тогда, согласно теореме о проекции (теорема 17.3 курса «Функциональный анализ. Часть 1»), существует элемент u ₀ ^ N, u ₀ ¹ 0. Возьмем произвольный элемент x Î H и построим элемент 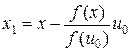. Так 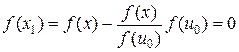, то x ₁ Î N. Тогда (x ₁, u ₀) = 0, т. е. 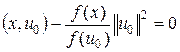, откуда f (x) = (x, u), где .

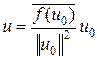Равенство || f || = || u || было доказано в примере 4.6.

Доказанная теорема утверждает, что между элементами гильбертова пространства H и его сопряженного H' существует биективное соответствие H ' u ® f_u Î H', где f_u (x) = (x, u). Очевидно, что это отображение обладает свойствами 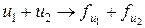, 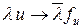(такие отображения называются антилинейными) и, так как || u || = || f_u ||, оно изометрично.

Значения линейных функционалов в R ⁿ являются координатами точки x в некоторой системе координат. С этой точки зрения можно рассматривать и линейные ограниченные функционалы в нормированном пространстве, т. е. значения линейных ограниченных функционалов в точке x считать координатами точки x и вместо x рассматривать ее «координаты» f (x). Поэтому можно считать, что введение сопряженного X' к бесконечномерному нормированному пространству X аналогично введению координат в геометрическом пространстве. Для обоснования правомерности такой точки зрения нужно прежде всего показать, что линейных ограниченных функционалов на нормированном пространстве достаточно много в том смысле, что по значениям всех линейных ограниченных функционалов точка x Î X определяется однозначно.