Теорема Банаха об обратном операторе и ее следствия

Среди теорем об обратных операторах особое место занимает теорема Банаха. Эта теорема вместе с теоремой Банаха – Штейнгауза и теоремой Хана – Банаха составляет три основных принципа линейного функционального анализа.

Теорема 2.4 (теорема об обратном операторе) (С. Банах). Пусть X и Y – банаховы пространства, A : X ® Y – линейный биективный ограниченный оператор. Тогда оператор A ^{– 1} является непрерывным.

Доказательство. Следует проверить, что для любого e > 0 образ шара B_X (0, e) Ì X при отображении A содержит некоторую окрестность нуля в Y, что и означает непрерывность A ^–1.

Пусть W Ì X – произвольная окрестность 0 в X. Прежде всего докажем, что замыкание 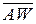содержит некоторую окрестность 0 в Y. Так как отображение X ´ X ' (x, y) → x – y Î X непрерывно, то существует такая окрестность нуля V, что V – V Ì W. Последовательность x / n → 0 для любого фиксированного x Î X и, следовательно, x Î n V для достаточно больших n. Поэтому

.

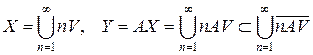По следствию 10.1 теоремы Бэра (курс «Функциональный анализ. Часть 1») одно из множеств 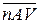содержит непустое открытое множество. Так как отображение Y ' y → n y Î Y является гомеоморфизмом, то и 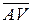содержит непустое открытое множество G. Таким образом,

.

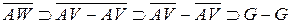Множество a – G открыто, так как отображение Y ' y → a – y Î Y является гомеоморфизмом. Поэтому и множество 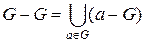открыто. Так как оно содержит 0, то оно является окрестностью нуля. Итак, замыкание образа окрестности нуля содержит некоторую окрестность нуля.

Зададим произвольное e ₀ > 0 и выберем e _i > 0 так, чтобы 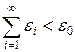. Согласно предыдущему, существует такая последовательность { h_i }, i = 0, 1,…, h_i > 0, что h_i → 0 и

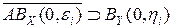. (3)

Покажем, что 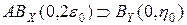. В самом деле, пусть 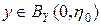. Тогда из (3) при i = 0 вытекает, что 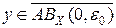. Это означает, что любой шар с центром в y пересекается с множеством 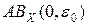, а значит, и

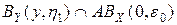¹ Æ.

Таким образом, существует точка 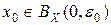такая, что 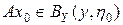, т. е. 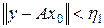, что означает 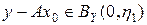. Аналогично из (3) при i = 1 вытекает существование 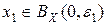такого, что 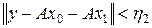. Продолжая это рассуждение, построим такую последовательность { x_n }, что 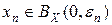и

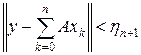. (4)

Положим s_n = x ₀ + … + x_n, тогда при n > m будем иметь

|| s_n – s_m || = || x_{m +1} + … + x_n || £ e_{m +1} + … + e_n.

Следовательно, { s_n } – последовательность Коши в X и поэтому ряд 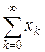сходится к некоторой точке x и 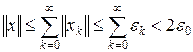, т. е. 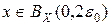. Так как оператор A непрерывен и h_{n +1} → 0 при n → ¥, то из (4) получаем, что y = A x. Отсюда 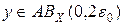. Теорема доказана.

Следствие 2.3. Пусть на линейном пространстве X заданы две нормы ||×||₁ и ||×||₂ и пространство X полно относительно каждой из норм. Если || x ||₁ £ C || x ||₂ для всех x Î X, то эти нормы эквивалентны, т. е. существует постоянная C ₁ > 0 такая, что || x ||₂ £ C ₁ || x ||₁ для всех x Î X.

Доказательство. Обозначим через X_k (k = 1, 2) банахово пространство X с нормой ||×|| _k. Неравенство || x ||₁ £ C || x ||₂ означает, что тождественный оператор I: X ₂ → X ₁ непрерывен. По теореме 2.4 оператор I ^{– 1}: X ₁ → X ₂ также непрерывен, что эквивалентно неравенству || x ||₂ £ C ₁ || x ||₁. Следствие доказано.

Для ряда приложений более удобным оказывается следствие, эквивалентное самой теореме, которое называется теоремой о замкнутом графике.

Определение 2.2. Пусть X и Y – нормированные пространства. Линейный оператор A, отображающий линейное подпространство D (A) Ì X в Y, называется замкнутым, если из того, что x_n → x ₀, x_n Î D (A) и A x_n → y ₀, следует, что x ₀ Î D (A) и y ₀ = A x ₀.

Требование замкнутости оператора эквивалентно тому, что его график является замкнутым множеством в X ´ Y.

Пример 2.2. Если A – ограниченный оператор, то A замкнут тогда и только тогда, когда замкнуто линейное подпространство, на котором он определен.

Пример 2.3. Пусть X = Y = C [0, 1|, D (A) = C ¹[0, 1| и оператор A есть оператор дифференцирования: A x (t) = x' (t). Если последовательность x_n состоит из дифференцируемых функций, равномерно сходится к функции x и последовательность производных 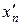равномерно сходится к функции y, то по известной теореме из математического анализа функция x непрерывно дифференцируема и x' = y. Это утверждение в точности означает, что оператор A замкнут в рассматриваемых пространствах. Приведенный пример показывает, что замкнутый оператор может быть неограниченным.

Теорема 2.5 (теорема о замкнутом графике). Пусть X и Y – банаховы пространства. Если линейный оператор A: X → Y определен на всем пространстве X и замкнут, то он ограничен.

Доказательство. На пространстве X введем новую норму || x ||₁ = || x || + || A x ||. Покажем, что относительно новой нормы пространство X полно. Пусть || x_n – x_m ||₁ → 0 при n, m → ¥. Тогда x_n есть последовательность Коши в X, а A x_n – последовательность Коши в Y. Значит, x_n → x, A x_n → y и в силу замкнутости оператора A x = y. Тогда || x_n – x ||₁ = || x_n – x ₀|| + || A x_n – y || → 0. В силу следствия 2.3 существует постоянная C такая, что || x ||₁ £ C || x ||, откуда получаем неравенство ограниченности || A x || £ C || x ||. Теорема доказана.

Пример 2.4. Пусть банахово пространство X разложено в прямую сумму своих замкнутых линейных подпространств Y и Z, т. е. каждый элемент x представляется в виде х = y + z. Определим проектор в X на подпространство Y по формуле P х = y. Покажем, что этот проектор является ограниченным оператором. В силу теоремы о замкнутом графике достаточно проверить замкнутость оператора P. Пусть x_n → x, P x_n → y. В силу замкнутости Y имеем y Î Y. Так как x_n – P x_n = z_n Î Z и z_n → z = х – y, в силу замкнутости Z получаем, что z Î Z и, значит, P х = y. Это и означает, что оператор P замкнут.

С помощью теоремы Банаха об обратном операторе можно получить другое доказательство теоремы Банаха – Штейнгауза.

Теорема 2.6 (С. Банах, Г. Штейнгауз). Пусть X – банахово пространство, Y – нормированное пространство и A_k Î L (X, Y) – линейные ограниченные операторы. Если для каждого x Î X 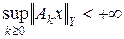, то .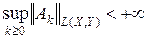

Доказательство. На банаховом пространстве X зададим еще одну норму 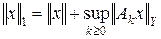. Из условия теоремы следует, что это действительно норма, причем очевидно, что || x || £ || x ||₁. Покажем, что в новой норме ||×||₁ пространство X полно. Действительно, пусть { z_n } – последовательность Коши в норме ||×||₁, т. е. для любого e > 0 найдется номер n ₀ такой, что при n, m ³ n ₀

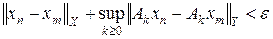. (5)

Отсюда следует, что { x_n } – последовательность Коши в X в исходной норме. Так как X полно, то существует x Î X такой, что || x_n – x || _X → 0 при n → ¥. Поскольку все A_k непрерывггы, то || A_k x_n – A_k x || → 0 при n → ¥ для любого k. Устремляя m к ¥ в неравенстве (5), получим

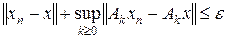
при n → ¥. Это означает, что || x_n – x ||₁ → 0 при n → ¥. Таким образом, X полно в норме ||×||₁. В силу следствия 2.3 эти нормы эквивалентны, т. е. существует постоянная C такая, что 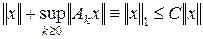. Отсюда 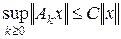для любого x Î X, т. е. || A_k || £ C. Теорема доказана.