Теорема Хана – Банаха о продолжении линейного функционала и ее следствия

Задача о том, достаточно ли много на нормированном пространстве линейных ограниченных функционалов, сводится к задаче о продолжении линейного функционала с подпространства на все пространство. Утверждение о возможности такого продолжения (теорема Хана – Банаха) дает решение этих задач. Эта теорема, как уже отмечалось, относится к числу трех основных принципов функционального анализа.

Определение 4.3. Пусть X – множество, { f_a } – семейство отображений f_a : X ® R. Будем говорить, что это семейство отображений разделяет точки пространства X, если для любой пары x ₁ ¹ x ₂ точек из X существует функция f Î { f_a } такая, что f (x ₁) ¹ f (x ₂).

Нужно выяснить, разделяют ли ограниченные линейные функционалы точки нормированного пространства, т. е. достаточно ли много таких функционалов.

Близкая к этой задаче – задача о продолжении линейного ограниченного функционала.

Определение 4.4. Пусть L Ì X – подпространство нормированного пространства X и пусть на L задан линейный ограниченный функционал f ₀. Продолжением функционала f ₀ называется линейный ограниченный функционал f на X такой, что f (x) = f ₀ (x) для x Î L.

Если для ограниченного функционала продолжение существует, то для x ₁ ¹ x ₂ Î X разделяющий их функционал построим следующим образом: на подпространстве L = { t (x ₁ – x ₂) : t Î K } зададим функционал f [ t (x ₁ – x ₂) ] = t. Его продолжение разделяет точки x ₁ и x ₂.

Отметим, что если f – продолжение f ₀, то

,

т. е. при продолжении норма не может уменьшиться. Представляют интерес такие продолжения, при которых норма не увеличивается.

Покажем, как эти задачи решаются в случае гильбертова пространства H на основе теоремы Рисса.

1. Если x ₁ ¹ x ₂, то для функционала f (x) = (x, x ₁ – x ₂) имеем f (x ₁) – f (x ₂) =
= || x ₁ – x ₂ || ² ¹ 0, т. е. линейные ограниченные функционалы разделяют точки пространства H.

2. Пусть L Ì H – подпространство в H и f ₀ – функционал на L. Согласно теореме Рисса, f ₀ (x) = (x, u ₀), где u ₀ Î L. Тогда формула f (x) = (x, u ₀) определяет линейный ограниченный функционал на H, являющийся продолжением f ₀, причем || f || = || f ₀ ||.

Основную теорему Хана – Банаха докажем в более общей формулировке.

Определение 4.5. Пусть X – линейное пространство. Полунормой на X называется отображение p : X ® R, удовлетворяющее следующим условиям:

1) p (x) ³ 0;

2) p (l x) = | l | p (x);

3) p (x + y) £ p (x) + p (y).

Примером полунормы является норма.

Теорема 4.2 (Х. Хан, С. Банах) (действительный случай). Пусть X – линейное пространство над R, p – полунорма на X, L ₀ Ì X – линейное подпространство и на L ₀ задан линейный функционал f ₀, удовлетворяющий условию

| f ₀ (x)| £ p (x), x Î L ₀.

Тогда существует линейный функционал F : X ® R такой, что F (x) = f ₀ (x) для x Î L ₀ и | F (x)| £ p (x) для всех x Î X.

Доказательство. Так как из неравенства F (x) £ p (x) следует | F (x)| £ p (x) (если F (x) < 0, то | F (x)| = F (– x) £ p (x) ), докажем существование продолжения, удовлетворяющего условию F (x) £ p (x).

Пусть x ₁ Ï L ₀. Множество L ₁ = { l x ₁ + x : x Î L ₀, l Î R } является подпространством в X.

Построим продолжение f ₁ функционала f ₀ на L ₁. В силу линейности f ₁ (l x ₁ + x) = l f ₁ (x ₁) + f ₁ (x), поэтому для определения f ₁ достаточно задать только число f ₁ (x ₁) = c. Нужно подобрать c так, чтобы выполнялось условие f ₁ (l x ₁ + x) £ p (l x ₁ + x), или

l c + f ₀ (x) £ p (l x ₁ + x) " x Î L ₀, l Î R. (4)

При l > 0 неравенство (4) переписывается следующим образом:

c £ p (x / l + x ₁) – f ₀ (x / l), (5)

а при l < 0 так:

– p ( – x / l – x ₁) + f ₀ ( – x / l) £ c. (6)

Покажем, что найдется постоянная c Î R, удовлетворяющая условиям (5) и (6). Пусть y', y" – произвольные элементы из L ₀. Тогда

f ₀ (y') + f ₀ (y") = f ₀ (y' + y") £ p (y' + y") £ p (y' – x ₁) + p (y" + x ₁),

или

– p (y' – x ₁) + f ₀ (y') £ p (y" + x ₁) – f ₀ (y"), (7)

Положим

,

.

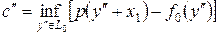Тогда из (7) вытекает, что c' £ c". Выбрав c так, чтобы c' £ c £ c", получаем, что c удовлетворяет условиям (5) и (6), т. е. функционал f ₁, определенный на L ₁ формулой f ₁ (l x ₁ + x) = l c + f ₀ (x), удовлетворяет условию подчинения f ₁ (l x ₁ + x) £ p (l x ₁ + x).

Рассмотрим теперь множество M всех продолжений g функционала f ₀, удовлетворяющих неравенству g (x) £ p (x). Продолжение f_a функционала f ₀ задается парой (L_a, f_a), состоящей из подпространства L_a и функционала f_a, определенного на нем. В множестве продолжений вводим отношение порядка: будем говорить, что (L_a, f_a) < (L_b, f_b), если L_a Ì L_b и f_a (x) = f_b (x) на L_a. Если в множестве M всех продолжений взять линейно упорядоченное подмножество (L_a, f_a) _{a Î A}, то, положив 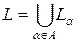и f (x) = f_a (x), для x Î L_a будем иметь, что (L, f) является верхней гранью для этого подмножества. Значит, согласно лемме Цорна, в множестве всех продолжений существует максимальный элемент 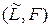. Если , то функционал F, согласно первой части теоремы, может быть продолжен и продолжение не является максимальным. Значит, максимальное продолжение есть продолжение на все пространство. Теорема доказана.

Теорема 4.3 (Х. Хан, С. Банах) (комплексный случай). Пусть X – линейное пространство над C, p – полунорма на X, L – линейное подпространство и на L задан линейный функционал f, удовлетворяющий условию

| f (x)| £ p (x) " x Î L.

Тогда существует линейный функционал F : X ® C такой, что 1) F (x) = f (x) для всех x Î L и 2) | F (x)| £ p (x) для всех x Î X.

Доказательство. Отметим, что если в комплексном линейном пространстве ограничиться умножением лишь на действительные числа, то это пространство можно рассматривать как действительное линейное пространство. Запишем f (x) = g (x) + i h (x), где g (x) и h (x) – действительная и мнимая части f (x) соответственно. Тогда g и h – действительные функционалы на L. Так как для каждого x Î L

g (i x) + i h (i x) = f (i x) = i f (x) = i [ g (i x) + i h (i x)] = – h (x) + i g (x),

то h (x) = – g (i x), поэтому f (x) = g (x) – i g (i x). Так как | g (x)| £ | f (x)| £ p (x), то по теореме 4.2 продолжим g до действительного функционала G : X ® R, удовлетворяющего условию G (x) £ p (x) при x Î X. Следовательно, – G (x) =
= G (– x) £ p (– x) = p (x) и поэтому | G (x)| £ p (x). Определим теперь функционал

F (x) = G (x) – i G (i x).

Это комплексный аддитивный функционал, определенный на X, однородный относительно умножения на действительные числа (ибо G – действительный линейный функционал). Чтобы доказать, что F – комплексный линейный функционал, достаточно показать, что F (i x) = i F (x) для всех x Î X. Действительно, F (i x) = G (i x) – i G (– x) = i G (x) + G (i x) = i [ G (x) – i G (i x)] = i F (x). Функционал F является продолжением f, так как G является продолжением g. Осталось доказать неравенство | F (x)| £ p (x). Запишем F (x) в виде F (x) = | F (x)| e ^ij, где j = arg F (x). Тогда | F (x)| = F (x) e ^{– ij} = F (e ^{– ij} x) ³ 0. Выражение F (e ^{– ij} x) является действительным и неотрицательным, поэтому

F (e ^{– ij} x) = | G (e ^{– ij} x)| £ p (e ^{– ij} x) = | e ^{– ij} | p (x) = p (x),

т. е. | F (x)| £ p (x). Теорема доказана.

Как следствие доказанных выше теорем получаем классическую теорему Хана – Банаха.

Теорема 4.4. Пусть X – нормированное пространство, L – его линейное подпространство. Тогда для любого ограниченного линейного функционала f : L ® C существует определенный на всем пространстве X ограниченный линейный функционал F такой, что 1) F является продолжением f; 2) || F || = || f ||.

Доказательство. Условие ограниченности | f (x)| £ || f || || x || есть частный случай условия 2) теоремы 4.3, так как p (x) = || f || || x || есть полунорма. Согласно теореме Хана – Банаха, существует продолжение F на все X такое, что | F (x)| £ || f || || x ||. Значит, || F || £ || f ||. Так как при продолжении норма не может уменьшиться, то получаем || F || = || f ||. Теорема доказана.

Следствие 4.1. Пусть x ₀ ¹ 0 – точка нормированного пространства X. Тогда существует линейный ограниченный функционал f на X такой, что f (x ₀) = || x ₀ || и || f || = 1.

Доказательство. Пусть L = { t x ₀ : t Î R } – одномерное подпространство, порожденное вектором x ₀. Определим на L функционал по формуле f ₀ (t x ₀) = t || x ₀ ||. Тогда f ₀ (x ₀) = || x ₀ || и так как | f ₀ (t x ₀)| = | t || x ₀ || | = 1×| t x ₀ ||, то || f ₀ || = 1. Согласно теореме 4.4, функционал f ₀ продолжается на все пространство с сохранением нормы. Следствие доказано.

Следствие 4.2. Линейные ограниченные функционалы разделяют точки нормированного пространства X, т. е. если x ₁ ¹ x ₂, то существует функционал f Î X' такой, что f (x ₁) ¹ f (x ₂).

Доказательство. Согласно следствию 4.2, для x ₀ = x ₁ – x ₂ существует функционал f такой, что f (x ₀) = || x ₀ || ¹ 0, тогда f (x ₁) – f (x ₂) = f (x ₀) ¹ 0. Следствие доказано.

Следствие 4.3. Пусть L – линейное подпространство нормированного пространства X и x ₀ Î X – внешняя точка для L. Тогда существует функционал f Î X' такой, что f (x) = 0 для x Î L и f (x ₀) ¹ 0.

Доказательство. Пусть L ₀ – линейное подпространство, порожденное L и x ₀, т. е. L ₀ = { y : y = t x ₀ + x, x Î L, t Î R }. Положим f ₀ (y) = t. Тогда f ₀ (x) = 0 для x Î L и f ₀ (x ₀) = 1 ¹ 0. Покажем, что функционал f ₀ ограничен. Для этого воспользуемся условием, что x ₀ – внешняя точка для L, т. е. существует r > 0 такое, что шар { x : || x – x ₀ || < r } не содержит точек из L. Значит, для любой точки x Î L выполнено неравенство || x – x ₀ || ³ r > 0. Тогда имеем || y || = || x + t x ₀ || =
= | t | || – x / t – x ₀ || ³ | t | r. Последнее неравенство справедливо потому, что – x / t Î L. Разделив на r это неравенство (так как r > 0), получаем | f ₀ (y)| = | t | £ (1 / r) || y ||, т. е. функционал f ₀ ограничен. По теореме Хана – Банаха его можно продолжить на все пространство X. Следствие доказано.

Замечание 4.1. Если L – замкнутое линейное подпространство в X, то x ₀ является внешней точкой тогда и только тогда, когда x ₀Ï L.

Определение 4.6. Последовательность функционалов { f_n } Ì X' называется биортогональной к последовательности { x_n } Ì X, если

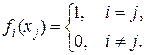
Следствие 4.4. Для любой конечной последовательности линейно независимых элементов x ₁, x ₂, ¼, x_n в нормированном пространстве существует биортогональная последовательность ограниченных функционалов.

Доказательство. На подпространстве 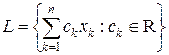функционал f_i зададим формулой f_i (x) = c_i, i = 1,¼, n. По теореме Хана – Банаха для нормированных пространств f_i можно продолжить на все X. Следствие доказано.

Следствие 4.5. Пусть x ₁, x ₂, ¼ – бесконечная последовательность точек нормированного пространства X и точка x_n не принадлежит замкнутому подпространству L_n, порожденному всеми остальными элементами последовательности. Тогда существует последовательность f ₁, f ₂, ¼ Î X', биортогональная к исходной.

Доказательство. Зафиксируем номер n. Пусть L_n – подпространство, порожденное x_k при k ¹ n. Точка x_n по условию не принадлежит L_n. Согласно следствию 4.4, существует функционал f_n такой, что f_n (L_n) = 0 и f_n (x_n) = l. Следствие доказано.

Замечание 4.2. В случае сепарабельного нормированного пространства теорема Хана – Банаха (теорема 4.4) может быть получена без использования леммы Цорна.

Доказательство. Пусть y ₁, y ₂, ¼, y_n, ¼ – счетное всюду плотное множество в X, состоящее из линейно независимых векторов. Все элементы y_k, не принадлежащие L, занумеруем в последовательность x ₁, x ₂, ¼, x_n, ¼ Пусть L_n – подпространство, порожденное L и элементами x ₁, x ₂, ¼, x_n. Согласно первой части теоремы Хана – Банаха, функционал f последовательно продолжаем с сохранением нормы на L ₁, L ₂, ¼, L_n и т. д. Получаем функционал, определенный на 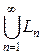– всюду плотном линейном подпространстве в X. По теореме о продолжении (см. раздел 10.4 курса «Функциональный анализ. Часть 1») функционал продолжаем на все пространство с сохранением нормы. Теорема доказана.

Пусть M Ì X'. Множество M ^{^} = { x : f (x) = 0 " f Î M } называется по аналогии со случаем гильбертова пространства ортогональным дополнением к M. Для множества N Ì X аналогично вводится ортогональное дополнение N ^{^} = { f : f Î X', f (x) = 0 " x Î N }.

Как уже отмечалось в разделе 14.2 курса «Функциональный анализ. Часть 1», замкнутое линейное подпространство в нормированном пространстве может не иметь дополнения. В качестве примера применения теоремы Хана – Банаха покажем, что конечномерное пространство всегда имеет дополнение.