Определение компактного оператора. Свойства компактных операторов

Лекция 8 Компактные операторы

8.1. Определение компактного оператора. Свойства компактных
операторов

8.2. Компактность интегральных операторов

8.3. Уравнения с компактными операторами. Фредгольмовы операторы

Как уже было отмечено, операторы в конечномерном пространстве обладают рядом свойств, которые не переносятся на произвольные ограниченные операторы в бесконечномерных пространствах. Например, утверждение, что если Ker A = {0}, то Im A = X, справедливо для линейного оператора A : X ® X в случае конечномерного пространства X и может быть неверным в бесконечномерном случае. В этом и последующих разделах будет изучен класс операторов, обладающих некоторыми свойствами операторов в конечномерных пространствах. Особый интерес к этому классу операторов связан также с тем, что в него входят многие интегральные операторы.

Определение 8.1. Пусть X и Y – банаховы пространства. Линейный оператор A : X ® Y называется компактным, или вполне непрерывным, если он любое ограниченное множество в X переводит в множество, предкомпактное в Y.

Напомним, что оператор A является ограниченным (непрерывным), если он ограниченное множество переводит в ограниченное. Выделение класса компактных операторов основано на том, что ограниченные множества могут не быть предкомпактными.

1^°. Если пространства X и Y конечномерны, то любой линейный оператор ограничен, значит, он переводит ограниченное множество в ограниченное; в конечномерном пространстве любое ограниченное множество предкомпактно. Таким образом, в конечномерных пространствах все линейные операторы компактны.

2^°. Пусть X и Y – произвольные нормированные пространства.

Определение 8.2. Линейный ограниченный оператор A : X ® Y называется оператором конечного ранга, если его образ Im A является конечномерным пространством.

Покажем, что операторы конечного ранга являются компактными. Пусть M Ì X – ограниченное множество, тогда множество A (M) Ì Y ограничено и в силу конечномерности Im A множество A (M) предкомпактно. В частности, если Y конечномерно, то любой ограниченный линейный оператор компактен.

3^°. Примером оператора конечного ранга является интегральный оператор с вырожденным ядром.

В пространстве C [0, 1] рассмотрим интегральный оператор с вырожденным ядром, т. е. оператор вида

,

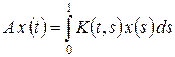где 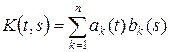, a_k (t), b_k (t) – непрерывные функции. Тогда

,

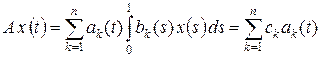т. е. образ Im A принадлежит конечномерному пространству 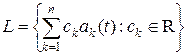, порожденному функциями a_k (t). Как интегральный оператор, A является ограниченным, следовательно, он компактен.

4^°. Для нулевого оператора образом является одна точка, значит, он компактен.

5^°. Тождественный оператор I в конечномерных пространствах является компактным (см. пример 1^°). Если пространство X бесконечномерно, то единичный шар в нем, согласно теореме Рисса (теорема 16.3 курса «Функциональный анализ. Часть 1»), не предкомпактен.

Оператор I переводит шар в себя, т. е. ограниченное множество в множество, не являющееся предкомпактным, значит, I не является компактным оператором.

6^°. Оператор вложения J : C ¹ [0, 1] ® C [0, 1] действует по формуле J x = x. Покажем, что J – компактный оператор. Пусть M – ограниченное множество в C ¹ [0, 1], т. е. || x ||₁ £ C. Покажем, что множество M предкомпактно в C [0, 1]. Согласно теореме Арцела – Асколи (теорема 13.5 курса «Функциональный анализ. Часть 1»), нужно проверить, что множество M равномерно ограничено и равностепенно непрерывно.

Для x Î M из условия || x ||₁ £ C получаем

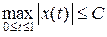, (1)

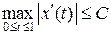, (2)

Неравенство (1) означает равномерную ограниченность множества M. Из неравенства (2) и оценки

| x (t ₁) – x (t ₂) | £ | x' (x) | | t ₁ – t ₂ | £ C | t ₁ – t ₂ |

получаем, что при d < e / C для любых x Î M и любых | t ₁ – t ₂ | < d имеем | x (t ₁) –
– x (t ₂) | < e, что означает равностепенную непрерывность множества M в C [0, 1]. Таким образом, множество M предкомпактно в C [0, 1] и оператор J компактен.

7^°. Оператор умножения на функцию a (t) в пространстве C [0, 1] и L_p [0, 1] не компактен, если a (t) ° 0.

Рассмотрим сначала случай пространства L_p [0, 1]. Пусть | x (t) | > 0 на множестве T ₀ Ì [0, 1], где m (T ₀) > 0. Тогда на бесконечномерном подпространстве L_p (T ₀) Ì L_p [0, 1], состоящем из функций, равных нулю вне множества T ₀, оператор A имеет ограниченный обратный. Как будет показано ниже, это невозможно, если A компактен.

Теперь рассмотрим случай пространства C [0, 1]. Пусть a (t ₀) ¹ 0 и a (t) Î C [0, 1]. Ограниченная последовательность sin n (t – t ₀) при умножении на a (t) переходит в последовательность a (t) sin n (t – t ₀), которая не является равностепенно непрерывной и, значит, не является предкомпактной.

Рассмотрим основные свойства компактных операторов.

Множество компактных операторов, действующих из банахова пространства X в банахово пространство Y, обозначим K (X, Y).

1. Если A и B – компактные операторы, то оператор A + B компактен.

Доказательство. Пусть M – ограниченное множество. В образе (A + B) (M) возьмем последовательность y_n = (A + B) (x_n). В силу компактности оператора A из последовательности A x_n можно выделить сходящуюся подпоследовательность 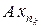, а в силу компактности B – из подпоследовательности 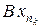сходящуюся подпоследовательность 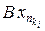. Подпоследовательность 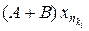сходится, значит, множество (A + B) (M) предкомпактно и оператор A + B компактен. Свойство доказано.

2. Пусть X, X ₁, Y, Y ₁ – банаховы пространства. Если A Î K (X, Y), B Î L (Y, Y ₁) и C Î L (X ₁, X), то операторы B A и A C компактны.

Доказательство. Действительно, если M – ограниченное множество в X, то A (M) предкомпактно и так как равномерно непрерывное отображение переводит предкомпактное множество в предкомпактное (см. замечание 13.1 курса «Функциональный анализ. Часть 1»), то B (A (M) ) предкомпактно в Y ₁.

Если M – ограниченное множество в X ₁, то C (M) – ограниченное множества в X и, поскольку оператор A компактен, A (C (M)) есть предкомпактное множество.

В частности, оператор умножения на число l ограничен и, значит, l A – компактный оператор.

3. Если последовательность A_n Î K (X, Y) компактных операторов сходится по норме к оператору A Î L (X, Y), то A – компактный оператор.

Доказательство. Пусть M – ограниченное множество в X и || x || £ C для x Î M. Для доказательства предкомпактности множества A (M) воспользуемся теоремой Хаусдорфа (теорема 13.1 курса «Функциональный анализ. Часть 1») и для любого e > 0 построим конечную e -сеть для множества A (M). Сначала выберем номер n ₀ так, чтобы 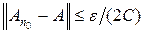. Множество 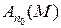предкомпактно. Пусть S = (s ₁, ¼, s_m) – конечная (e / 2)-сеть для 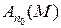. Покажем, что S является e -сетью для A (M). Пусть y Î A (M), т. е. y = A x, x Î M. Существует s_i такое, что 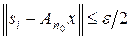. Тогда

,

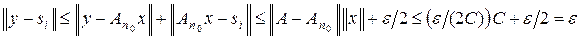что и требовалось доказать.

4. Оператор, сопряженный к компактному, является компактным.

Доказательство. Если A Î K (X, Y), то L (Y', X'). Пусть M – ограниченное множество в Y' и || f || £ c для f Î M. Тогда для g = A' f имеем

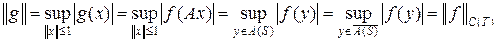, (3)

где S – единичный шар в X, 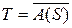. Множестю A (S) предкомпактно, a 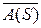компактно в Y. Функционалу g поставим в соответствие сужение функционала f на множество T, т. е. элемент пространства C (T) непрерывных функций. Формула (3) показывает, что это соответствие изометрично. Поэтому достаточно доказать предкомпактность в C (T) множества M функционалов f, для чего проверим выполнение условий теоремы 13.5 курса «Функциональный анализ. Часть 1». Действительно, для y Î T | f (y) | £ || f || || y || £ c || A || || x || £ c || A ||, т. е. M равномерно ограничено.

Если при e > 0 выберем d = e / c, то из неравенства || y ₁ – y ₂ || < d следует, что | f (y ₁) – f (y ₂) | £ || f || || y ₁ – y ₂ || £ c × e / c, т. е. множество M равностепенно непрерывно в C (T). Свойство доказано.

Из свойств 1 – 3 следует, что множество K (X, Y) компактных операторов является замкнутым линейным подпространством в пространстве L (X, Y) линейных ограниченных операторов.

Из 2^° и свойства 3 следует, что предел последовательности операторов конечного ранга является компактным оператором. Для гильбертовых пространств (и банаховых со счетным базисом) верно и обратное: любой компактный оператор является пределом сходящейся по норме последовательности операторов конечного ранга A_n = P_n A P_n, где P_n – проектор на первые n базисных векторов.

Существуют сепарабельные банаховы пространства, в которых есть компактные операторы, не являющиеся пределами последовательностей операторов конечного ранга. Впервые пример такого пространства был построен П. Энфло в 1972 году и тем самым было получено решение известной проблемы С. Банаха.