Покажем, что если функции K (t, s) удовлетворяют некоторым условиям, то интегральные операторы с ядром K (t, s) являются компактными в соответствующих пространствах.
Теорема 8.1. Пусть W – ограниченная область в R n и пусть K (t, s) – функция, определенная на 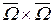 и удовлетворяющая следующим условиям:
и удовлетворяющая следующим условиям:
1) существует постоянная C такая, что
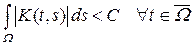 ;
;
2) для любого e > 0 существует d > 0 такое, что из неравенства | t 1 –
– t 2 | < d следует 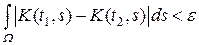 .
.
Тогда интегральный оператор, действующий по формуле
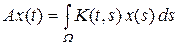 ,
,
компактен в 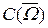 .
.
Доказательство. Так же, как и в примере 15.6 курса «Функциональный анализ. Часть 1», проверяем, что оператор A действует из 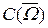 в
в 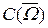 и ограничен. Возьмем ограниченное множество M в
и ограничен. Возьмем ограниченное множество M в 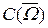 , т. е.
, т. е. 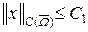 для x Î M. Тогда множество A (M) ограничено в
для x Î M. Тогда множество A (M) ограничено в 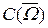 . Для доказательства предкомпактности множества A (M) достаточно показать в силу теоремы 13.5 курса «Функциональный анализ. Часть 1», что оно равностепенно непрерывно. Проверим равностепенную непрерывность A (M). Для e / C 1 > 0 возьмем d > 0 из условия 2) теоремы 8.1. Тогда если | t 1 – t 2 | < d / C 1, то
. Для доказательства предкомпактности множества A (M) достаточно показать в силу теоремы 13.5 курса «Функциональный анализ. Часть 1», что оно равностепенно непрерывно. Проверим равностепенную непрерывность A (M). Для e / C 1 > 0 возьмем d > 0 из условия 2) теоремы 8.1. Тогда если | t 1 – t 2 | < d / C 1, то
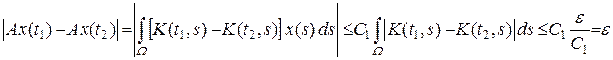 .
.
Теорема доказана.
Следствие 8.1. Если K (t, s) – непрерывная функция двух переменных в ограниченной замкнутой области 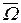 Ì R n, то интегральный оператор с ядром K (t, s) компактен в
Ì R n, то интегральный оператор с ядром K (t, s) компактен в 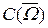 .
.
Доказательство. Проверим выполнение условий 1) и 2) теоремы 8.1. Условие 1) следует из ограниченности функции K (t, s). В силу равномерной непрерывности функции K (t, s) для любого e > 0 существует d > 0 такое, что для любых t 1 – t 2 Î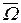 и удовлетворяющих условию | K (t 1, s) – K (t 2, s) | < e / m (W) выполнено | t 1 – t 2 | < d. Тогда
и удовлетворяющих условию | K (t 1, s) – K (t 2, s) | < e / m (W) выполнено | t 1 – t 2 | < d. Тогда 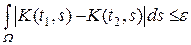 и условие 2) выполнено. Следствие доказано.
и условие 2) выполнено. Следствие доказано.
Замечание 8.1. В условиях следствия компактность оператора A можно доказать следующим образом. Согласно теореме Вейерштрасса, существует последовательность многочленов Kn (t, s), равномерно сходящаяся к непрерывной функции K (t, s) на 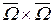 . Интегральные операторы конечного ранга
. Интегральные операторы конечного ранга
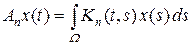
сходятся по норме к оператору A (см. пример 1.1). Оператор A компактен как предел последовательности компактных операторов.
Теорема 8.2. Пусть (T, S, m) – пространство с конечной или s -конечной мерой, функция K (t, s) Î L 2 (T ´ T), т. е. она измерима и
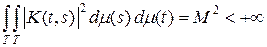 .
.
Тогда интегральный оператор с ядром K (t, s) компактен в пространстве L 2 (T, m).
Доказательство. Согласно примеру 1.2, интегральный оператор A является пределом по норме интегральных операторов An конечного ранга. Следовательно, A компактен. Теорема доказана.
Следствие 8.2. Если W – ограниченная область в R n и ядро K (t, s) непрерывно на 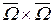 , то интегральный оператор с ядром K (t, s) компактен в L 2 (W).
, то интегральный оператор с ядром K (t, s) компактен в L 2 (W).
Интегральные операторы, удовлетворяющие условиям теоремы, называются операторами Гильберта – Шмидта.
Приведем один из результатов для пространств Lp.
Теорема 8.3. Пусть W – ограниченная область в R n и пусть ядро K (t, s) непрерывно в 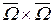 . Тогда интегральный оператор A с ядром K (t, s) является компактным оператором в Lp (W) при 1 £ p < + ¥.
. Тогда интегральный оператор A с ядром K (t, s) является компактным оператором в Lp (W) при 1 £ p < + ¥.
Доказательство. Пусть M – ограниченное множество в Lp (W). Покажем, что множество A (M) предкомпактно в Lp (W).
Пусть 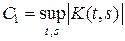 и
и 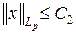 для x Î M. Тогда
для x Î M. Тогда
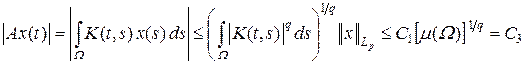 ,
,
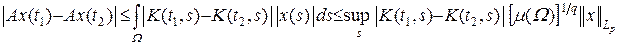 .
.
В силу равномерной непрерывности функции K (t, s) по e 1 = e [ m (W)] – 1/ q (C 2) – 1 можно найти e > 0 такое, что при | t 1 – t 2 | < d выполняется | A x (t 1) – A x (t 2) | < e. Это означает, что множество A (M) принадлежит 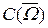 и предкомпактно в нем. Тогда у любой последовательности A xn, xn Î M, существует равномерно сходящаяся подпоследовательность, а из равномерной сходимости следует сходимость в Lp (W). Следовательно, A (M) предкомпактно в Lp (W). Теорема доказана.
и предкомпактно в нем. Тогда у любой последовательности A xn, xn Î M, существует равномерно сходящаяся подпоследовательность, а из равномерной сходимости следует сходимость в Lp (W). Следовательно, A (M) предкомпактно в Lp (W). Теорема доказана.
Замечание 8.2. Для других классов ядер проверку компактности в Lp (W) можно проводить с помощью критерия предкомпактности множества в Lp (W) (см. теорему 13.9 курса «Функциональный анализ. Часть 1») или с помощью аппроксимации операторами конечного ранга.
Замечание 8.3. В ходе доказательства теоремы 8.3 установлено следующее свойство: если ядро K (t, s) непрерывно в 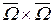 и функция x Î Lp (W), где W – ограниченная область в R n, то
и функция x Î Lp (W), где W – ограниченная область в R n, то 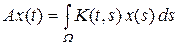 является непрерывной функцией.
является непрерывной функцией.
Теорема 8.4. Интегральный оператор 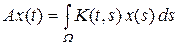 со слабополярным ядром K (t, s) компактен в пространстве C [ a, b ].
со слабополярным ядром K (t, s) компактен в пространстве C [ a, b ].
Доказательство. В примере примере 1.4 построена последовательность непрерывных функций Kn (t, s) такая, что интегральные операторы An с ядрами Kn (t, s) сходятся по норме к оператору A. Операторы An компактны в силу следствия 8.1 теоремы 8.1 и, значит, компактен оператор A как предел последовательности компактных операторов. Теорема доказана.
Замечание 8.4. В случае пространства R n ядро интегрального оператора K (t, s) называется слабополярным, если оно может быть представлено в виде
K (t, s) = K 0 (t, s)| t – s | – a, (4) где a < n, 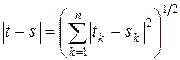 расстояние между точками t и s в R n, K 0 (t, s) – непрерывная функция. Аналогично теореме 8.4 получаем, что если W – ограниченная область в R n, то интегральный оператор со слабополярным ядром компактен в пространстве
расстояние между точками t и s в R n, K 0 (t, s) – непрерывная функция. Аналогично теореме 8.4 получаем, что если W – ограниченная область в R n, то интегральный оператор со слабополярным ядром компактен в пространстве 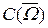 .
.
Теорема 8.5. Пусть W – ограниченная область с R n и пусть ядро K (t, s) представляется в виде (4), где a < n /2 и K 0 (t, s) – ограниченная измеримая функция. Тогда интегральный оператор с ядром K (t, s) компактен в пространстве L 2(W).
Доказательство. Согласно теореме 8.2, достаточно проверить, что
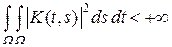 .
.
Пусть | K 0 (t, s) | £ C 1 и | t – s | £ R для любых t и s из W. Тогда
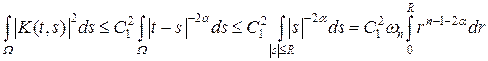 , (5)
, (5)
где 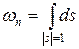 – площадь единичной сферы в пространстве R n. В силу условия a < n /2 последний интеграл в (5) существует и справедливо неравенство
– площадь единичной сферы в пространстве R n. В силу условия a < n /2 последний интеграл в (5) существует и справедливо неравенство
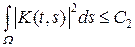 , (6)
, (6)
из которого после интегрирования по t получаем (4). Теорема доказана.
Замечание 8.5. Слабополярное ядро при a < n /2 удовлетворяет условию (6), более сильному, чем необходимо для компактности оператора A. Это условие будет использовано далее в теореме Гильберта – Шмидта.
Приведем пример интегрального оператора, который не является компактным. Пусть K Î L 1(R) и оператор A действует в L 2(R) по формуле
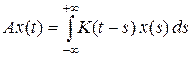 .
.
После преобразования Фурье оператор A перейдет в оператор 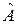 умножения на функцию
умножения на функцию 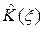 , который не является компактным (см. п. 7° раздела 8.1).
, который не является компактным (см. п. 7° раздела 8.1).
Замечание 8.6. Условие a < n в замечании 8.3 существенно: если a = n и K 0 (t, s) ¹ 0, то интегральный оператор с ядром K (t, s) не является даже ограниченным в пространстве 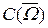 .
.
Замечание 8.7. Если компактный оператор A : X ® X имеет ограниченный обратный A – 1, то тождественный оператор I = A A – 1 по свойству 2 раздела 8.1 является компактным и, значит, пространство X конечномерно. Поэтому для уравнений A x = y с компактным оператором A в бесконечномерных пространствах всегда неверна теорема существования и единственности решения. Это относится, в частности, к интегральным уравнениям первого рода
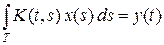
в случае, если K (t, s) обеспечивает компактность оператора A.
 2014-02-09
2014-02-09 2391
2391