Формула A' f (x) = f (A x) задает явно действие сопряженного оператора на функционалах, поэтому построение сопряженного оператора сводится к подстановке A в формулу A' f (x) = f (A x). На практике, однако, в тех случаях, когда известны теоремы об общем виде функционала, вместо пространства функционалов рассматривают изоморфное ему другое, более удобное для вычислений пространство. Пусть функционал f Î Y' представляется через элемент u пространства Y 1. Значение функционала f (x) будем обозначать
f (x) = á u, x ñ. (1)
Тогда f (A x) = á u, A x ñ. Обозначим через A' u Î X 1 элемент, соответствующий функционалу A' f Î X'. Тогда равенство A' f (x) = f (A x) запишется в виде
á A' u, x ñ = á u, A x ñ. (2)
Таким образом, сопряженный оператор A' можно определить как оператор A' : Y 1 ® X 1, удовлетворяющий равенству (2).
Например, в случае пространства Lp (T, m) вместо пространства ограниченных линейных функционалов рассматриваем изоморфное ему пространство Lq (T, m), где 1 / p + 1 / q = 1. Заметим, что вид сопряженного оператора зависит от способа реализации сопряженного пространства. Например, изоморфизм между Lq (T, m) и (Lp (T, m) ) ' можно задать формулой
|
|
|
Lq (T, m) ' u ®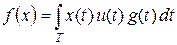 ,
,
где g (t) – фиксированная измеримая функция такая, что | g (t) | = l. При таком представлении сопряженный оператор будет иметь несколько иной вид, чем, например, в 2° и 3°.
1°. Пусть X = C n, Y = C m и линейный оператор A : X ® Y задается m ´ n -матрицей с элементам (aij) обычной формулой 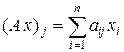 . Пространство, сопряженное к C m, реализуется как пространство C m с помощью соответствия
. Пространство, сопряженное к C m, реализуется как пространство C m с помощью соответствия
C m ' x «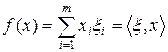 .
.
Поэтому из формулы (2) получаем
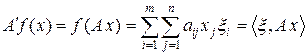 .
.
Построенный новый функционал представим в виде
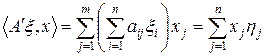 ,
,
где
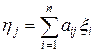 . (3)
. (3)
Таким образом, функционал, соответствующий вектору x, перешел под действием сопряженного оператора в функционал, соответствующий вектору h. В этом смысле будем говорить, что сопряженный оператор отображает вектор x в вектор h, т. е. сопряженный оператор действует по формуле (3), из которой видим, что действие оператора задается матрицей (aji), транспонированной к матрице (aij).
Применим к данному случаю теорему 6.2. Так как в конечномерном пространстве любое линейное подпространство замкнуто (теорема 16.1 курса «Функциональный анализ. Часть 1»), из следствия 6.1 получаем следующую фундаментальную теорему, дающую условия разрешимости системы линейных алгебраических уравнений.
Теорема 6.4. Для того, чтобы система линейных алгебраических уравнений
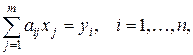
имела решение для данного вектора y = (y 1, ¼, yn), необходимо и достаточно, чтобы 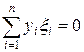 для любого вектора x = (x 1, ¼, xn), являющегося решением однородной транспонированной системы
для любого вектора x = (x 1, ¼, xn), являющегося решением однородной транспонированной системы
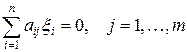 .
.
2°. Рассмотрим в пространстве Lp [0, 1] интегральный оператор
|
|
|
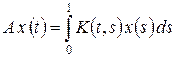 ,
,
где K (t, s) – ограниченная измеримая функция. Построим оператор, сопряженный к оператору A. Любой функционал f Î (Lp [0, 1] ) ' представляется в виде
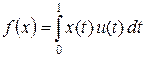 ,
,
где u Î Lq [0, 1] (см. раздел 5.6). Возьмем элемент u Î Lq [0, 1] и посмотрим, как действует оператор A' на соответствующий ему функционал
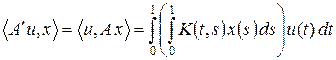 .
.
Переставив порядок интегрирования в последнем интеграле (что законно в силу теоремы Фубини), получим
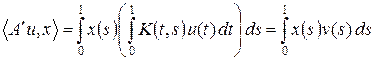 ,
,
где 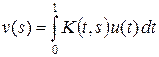 . Таким образом, сопряженный оператор A' переводит функционал, соответствующий функции u, в функционал, соответствующий функции v, т. е. сопряженный оператор действует по формуле
. Таким образом, сопряженный оператор A' переводит функционал, соответствующий функции u, в функционал, соответствующий функции v, т. е. сопряженный оператор действует по формуле
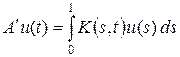 .
.
Таким образом, оператор, сопряженный к интегральному оператору с ядром K (t, s), является интегральным оператором с ядром K (s, t). Такое ядро называется транспонированным к ядру K (t, s). Аналогичный результат справедлив в пространствах Lp (T, m), а также для ограниченных интегральных операторов, заданных с помощью неограниченных ядер.
Как известно, интегральное уравнение Фредгольма
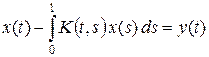 (4)
(4)
может не иметь решения для некоторых y (t). Получим условия разрешимости этого уравнения, опираясь на теорему 6.2.
Теорема 6.5. Для того, чтобы уравнение (4) имело решение x Î Lp [0, 1], для данного y Î Lp [0, 1] необходимо, чтобы 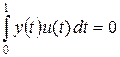 для любой функции u Î Lq [0, 1], удовлетворяющей однородному сопряженному уравнению
для любой функции u Î Lq [0, 1], удовлетворяющей однородному сопряженному уравнению
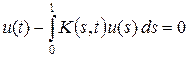 .
.
Доказательство того, что указанное условие является достаточным, требует более тонких рассуждений.
Определение 6.2. Ядро K (t, s) интегрального уравнения (4) называется вырожденным, если оно может быть представлено в виде
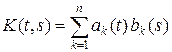 .
.
Пример 6.1. Рассмотрим уравнение
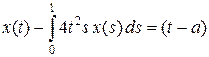 . (5)
. (5)
Запишем однородное сопряженное уравнение
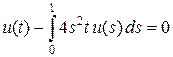 . (6)
. (6)
Это уравнение с вырожденным ядром. Его решение будем искать в виде u (t) = c t. Подставляем u в уравнение (6), получаем 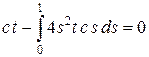 , откуда 0 = 0, т. е. для любого c функция c t является решением уравнения (6). Из теоремы 6.5 получаем, что условие разрешимости уравнения (5) имеет вид
, откуда 0 = 0, т. е. для любого c функция c t является решением уравнения (6). Из теоремы 6.5 получаем, что условие разрешимости уравнения (5) имеет вид 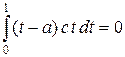 . Или, вычисляя, получаем c (1/ 3 – a / 2) = 0. Отсюда видим, что при a = 2/ 3 условие выполнено, а при a ¹ 2/ 3 условие не выполнено и уравнение (5) решения не имеет.
. Или, вычисляя, получаем c (1/ 3 – a / 2) = 0. Отсюда видим, что при a = 2/ 3 условие выполнено, а при a ¹ 2/ 3 условие не выполнено и уравнение (5) решения не имеет.
3°. Рассмотрим оператор Ta : Lp [0, 1] ® Lp [0, 1], 1 £ р < + ¥, вида Ta x (t) = x (a (t) ), где a : [0, 1] ® [0, 1] – непрерывно дифференцируемое обратимое отображение отрезка [0, 1] в себя, a' (t) ¹ 0. Построим сопряженный оператор 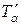 :
:
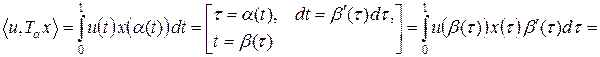
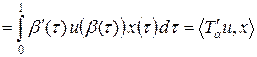 .
.
Получаем, что сопряженный оператор 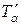 действует в Lq [0, 1] по формуле
действует в Lq [0, 1] по формуле 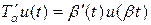 , где b = a – 1.
, где b = a – 1.
 2014-02-09
2014-02-09 2860
2860
