Спектр оператора

Лекция 7 Спектр оператора. Слабая сходимость. Рефлексивность

7.1. Спектр оператора

7.2. Слабая сходимость. Рефлексивность

Введем понятие спектра оператора, которое обобщает понятие множества собственных чисел матрицы.

Определение 7.1. Пусть A : X ® X – ограниченный оператор и банаховом пространстве X над полем C. Точка l Î C называется регулярной точкой оператора A, если оператор (l I – A)^{– 1} существует и является ограниченным оператором, определенным на всем X. Множество регулярных точек обозначается r (A) и называется резольвентным множеством оператора A.

Определение 7.2. Комплексное число l, не являющееся регулярным, называется спектральным. Множество спектральных точек s (A) оператора A называется спектром оператора A. Таким образом, s (A) = C \ r (A).

Определенная на r (A) функция (l I – A)^{– 1} называется резольвентой оператора A и обозначается R (l; A). Значениями этой функции являются ограниченные операторы.

Теорема 7.1. Резольвентное множество r (A) оператора A открыто. Функция R (l; A) – операторнозначная аналитическая функция в r (A).

Доказательство. Пусть l – фиксированная точка в r (A) и m – любое комплексное число такое, что | m | < || R (l; A) ||^{– 1}. Покажем, что l + m Î r (A). Это означает, что множество r (A) открыто. В самом деле,

(l + m) I – A = m I + (l I – A) = (l I – A) [ I + m R (l; A)]. (1)

В силу теоремы 2.3 и условия на m оператор, стоящий в правой части равенства (1), имеет ограниченный обратный оператор

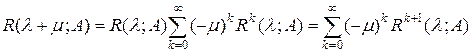. (2)

Равенство (2) показывает, что функция R (l; A) в окрестности каждой точки l Î r (A) разлагается в степенной ряд, т. е. R (l; A) есть операторная аналитическая функция на r (A). Теорема доказана.

Теорема 7.2. Спектр ограниченного оператора A есть непустое компактное множество в C.

Доказательство. Покажем, что s (A) Ì { l Î C : | l | £ || A ||}. Если | l | > || A ||, то в силу теоремы 2.2 оператор (l I – A) = l (I – A / l) обратим и

(l I – A)^{– 1} = l ^{– 1} (I – A / l)^{– 1} =.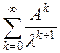

Следовательно,

|| R (l; A) || £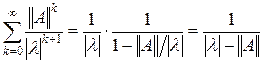 (3)

при | l | > || A ||.

Так как резольвентное множество r (A) открыто, s (A) – замкнутое ограниченное множество в C, т. е. компактное множество. Покажем, что s (A) ¹ Æ. Предположим противное. Тогда r (A) = C. Следовательно, согласно теореме 7.1, R (l; A) есть целая функция, т. е. функция аналитическая на всем C. Поэтому она ограничена на множестве D = { l Î C : | l | £ 2 || A ||}. Согласно неравенству (3), она ограничена и вне множества D. Значит, || R (l; A) || £ c для всех l Î C. Причем из (3) следует, что || R (l; A) || ® 0 при | l | ® ¥. Таким образом, для любого x Î X и каждого f Î X' функция j (l) = f ( R (l; A) x) есть целая аналитическая функция, ограниченная и стремящаяся к нулю на бесконечности. По теореме Лиувилля получаем, что j (l) = 0 для всех x Î X и всех f Î X' и из следствия 4.1 теоремы Хана – Банаха вытекает, что R (l; A) = 0 для любого l Î C. Отсюда следует, что I = (l I – A) R (l; A) = 0. Противоречие доказывает теорему.

Теорема 7.3. Спектр сопряженного оператора A' : X' ® X' совпадает со спектром оператора A : X ® X. Кроме того, R (l; A') = R (l; A) ' для чисел l Î r (A) = r (A' ).

Доказательство. Это утверждение является непосредственным следствием свойства сопряженного оператора (см. раздел 6.1). Теорема доказана.

В силу теоремы Банаха об обратном операторе существование ограниченного обратного к оператору l I – A эквивалентно тому, что Im (l I – A) = X и Ker (l I – A) = {0}. Число l является точкой спектра оператора A, если нарушено хотя бы одно из этих условий. В зависимости от того, какое из условий нарушено, выделяются следующие типы точек спектра.

1. Число l называется собственным значением оператора A, если Ker (l I – A) ¹ {0}, т. е. существует ненулевой вектор x такой, что A x = l x. Такой вектор называется собственным вектором оператора A, соответствующим собственному значению l. Множество собственных значений называется точечным спектром.

2. Число l называется точкой непрерывного спектра оператора A, если Ker (l I – A) = {0}, Im (l I – A) ¹ X, .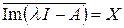

3. Число l называется точкой остаточного спектра оператора A, если Ker (l I – A) = {0} и .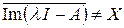

Таким образом, вся комплексная плоскость разбивается на четыре попарно непересекающихся множества: резольвентное множество, точечный, непрерывный и остаточный спектр.

Замечание 7.1. Аналогичным образом можно ввести понятие спектра оператора в случае пространств над полем вещественных чисел. Однако в этом случае спектр может оказаться пустым.

Пример 7.1. Пусть X = C ⁿ и A : X ® X – линейный оператор, заданный матрицей M. Оператор l I – A обратим тогда и только тогда, когда невырождена матрица l E – M, т. е. r (l) = det (l E – M) ¹ 0. Таким образом, спектр оператора A состоит из корней характеристического многочлена r (l). Каждый из этих корней является собственным значением оператора A, и, значит, весь спектр оператора в конечномерном пространстве точечный, а непрерывный и остаточный спектры пусты.

Пример 7.2. Пусть X = C [0, 1], A x (t) = t x (t). Если A x = l x, т. е. t x (t) = l x (t), то (t – l) x (t) º 0, откуда x (t) º 0. Значит, у оператора A нет собственных значений и точечный спектр пуст. Если l Ï [0, 1], то функция 1/ (l – t) непрерывна на [0, 1] и для любой функции y Î C [0, 1] функция x (t) = y (t) / (l – t) непрерывна и является решением уравнения (l I – A) x = y. Значит, все точки l, лежащие вне отрезка |0, 1], являются регулярными точками оператора A. Пусть теперь l – точка отрезка [0, 1]. Если y (t) = (l – t) x (t), где x Î C [0, 1], то y (l) = 0. Для функции y ₀(t) º 1 получаем r (y, y ₀) ³ 1. Это значит, что образ оператора l I – A, состоящий из таких функций y, имеет внешние точки и, следовательно, не является всюду плотным в C [0, 1]. Значит, все точки отрезка [0, 1] являются точками остаточного спектра.

Пример 7.3. X = L_p [0, 1], 1 £ р < + ¥, и A x (t) = t x (t). Как и в примере 7.2, получаем, что у оператора A нет собственных значений и если l Ï [0, 1], то l является регулярным значением. Покажем, что все точки отрезка [0, 1] являются точками непрерывного спектра. Если при некотором y уравнение
(l I – A) x = y имеет решение, то x (t) = y (t) / (l – t). При y ₀(t) º 1 получаем, что x (t) = 1/ (l – t) и не принадлежит пространству L_p [0, 1] при 0 £ l £ 1. Значит, функция y ₀ не принадлежит Im (l I – A) при 0 £ l £ 1 и весь отрезок состоит из спектральных значений. Покажем, что образ Im (l I – A) всюду плотен в пространстве L_p [0, 1]. Если функция y (t) = 0 в окрестности точки l Î [0, 1], то она является образом функции x (t) = y (t) / (l – t), принадлежащей L_p [0, 1]. Для любой функции y Î L_p [0, 1] построим функцию

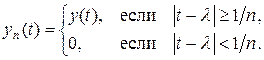
Тогда || y – y_n || ® 0 при n ® ¥ в силу абсолютной непрерывности интеграла Лебега. Функции y_n принадлежат образу Im (l I – A), и, значит, 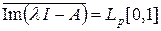. Таким образом, все точки отрезка [0, 1] являются точками непрерывного спектра.

Пример 7.4. Пусть X = l_p, 1 £ р £ + ¥, и оператор A задан формулой A x = (x ₂, x ₃, ¼) (оператор сдвига). Так как || A || = 1, спектр оператора A лежит в круге радиуса 1. Если A x = l x, то x = (x ₁, l x ₁, l ² x ₁, ¼). При р < + ¥ построенная последовательность принадлежит l_p тогда и только тогда, когда | l | < 1. Если р = + ¥, то построенная последовательность принадлежит l _¥, тогда и только тогда, когда | l | £ 1. Таким образом, при р = + ¥ спектр оператора A есть единичный круг D = { l : | l | £ 1}, причем все точки спектра являются собственными значениями. При р < + ¥ все внутренние точки круга D – собственные значения оператора A и в силу замкнутости спектра s (A) = D (спектром оператора является весь единичный круг). Покажем, что при р < + ¥ точки l, лежащие на окружности | l | = 1 – это точки непрерывного сгектра, т. е. покажем, что образ Im (l I – A) всюду плотен в l_p. Согласно следствию 6.3 теоремы 6.2, для этого достаточно показать, что Ker (l I – A' ) = {0}. Для оператора A сопряженный A' действует в пространстве l_q, где 1 / p + 1 / q = 1 при 1 < р < + ¥ и q = + ¥ при р = 1, и имеет вид A' u = (0, u ₁, u ₂, ¼). Если A' u = l u для некоторой последовательности u = (u ₁, u ₂, ¼), то 0 = l u ₁, u ₁ = l u ₂, ¼ и, следовательно, u = 0. Значит, Ker (l I – A' ) = {0}, и при 1 £ р < + ¥ окружность | l | = 1 состоит из точек непрерывного спектра.