2014-02-09
666
Для его получения используем ту же упрощенную схему, что и для уравнений движения газа: будем рассматривать изменение внутренней энергии фиксированной массы газа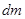 
за короткий промежуток времени 
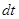. Так как по сделанным допущениям в веществе отсутствует теплопроводность, вязкость и источники (стоки) энергии, то это изменение вызывается лишь работой сил давления на гранях куба при его сжатии или расширении. Работа давления, связанная с движением граней объема вдоль оси 
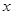, очевидно, равна
,
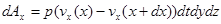где слагаемые в скобках можно, отбрасывая члены второго порядка малости, переписать через производную 
и получить
.
Здесь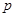 
– среднее давление в элементарном объеме. Аналогично
,
.
Полная работа, совершенная над газом за время 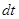, есть
.
Она равна изменению внутренней энергии объема, т.е.
,
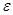- удельная внутренняя энергия. Приравняв оба выражения для 
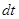и устремив к нулю , окончательно получим
, (14)
где 
- полная (субстанциональная) производная внутренней энергии по времени. Заметим, что с помощью новых уравнений (14) приводится, подобно (4), к дивергентному виду
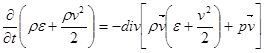. (15)
Слева в (15) стоит производная от полной (внутренней и кинетической) энергии газа в данной точке пространства. Так как термодинамические свойства вещества предполагаются известными, то 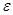- известная функция уже введенных величин 
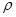и 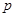, и уравнение (14) либо (15) дает недостающую связь для определения искомых газодинамических величин.
