Признаком называется отображение f: X → Df, где Df – множество допустимых значений признака. Если заданы признаки f 1, f 2, … fn, то вектор x = f (x)1, f (x)2, … fn (x) называется признаковым описанием объекта x  Х. Признаковые описания допустимо отождествлять с самими объектами. При этом множество X = Df1 × Df2 ×…× Dfn называют признаковым пространством.
Х. Признаковые описания допустимо отождествлять с самими объектами. При этом множество X = Df1 × Df2 ×…× Dfn называют признаковым пространством.
В зависимости от множества Df признаки делятся на следующие типы:
· бинарный признак: Df = {0, 1};
· номинальный признак: Df – конечное множество;
· порядковый признак: Df – конечное упорядоченное множество;
· количественный признак: Df – множество действительных чисел.
Часто встречаются прикладные задачи с разнотипными признаками, для их решения подходят далеко не все методы.
Типы описаний объекта
1. Признаковое описание является наиболее распространенным случаем. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми, текстовыми или качественными.
2. Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов обучающей выборки. С этим типом данных работают некоторые методы, в частности метод ближайших соседей и метод потенциальных функций.
3. Временной ряд или сигнал представляет собой последовательность измерений во времени. Каждое измерение может быть представлено числом, вектором, а в общем случае – признаковым описанием исследуемого объекта в данный момент времени.
4. Изображение или видеоряд.
5. Сложное описание, когда данные представляют в виде графов, текстов, результатов запросов к базе данных и т.д. Путем предварительной обработки и извлечения признаков это описание, как правило, приводится к первому или второму типу.
Типы классов
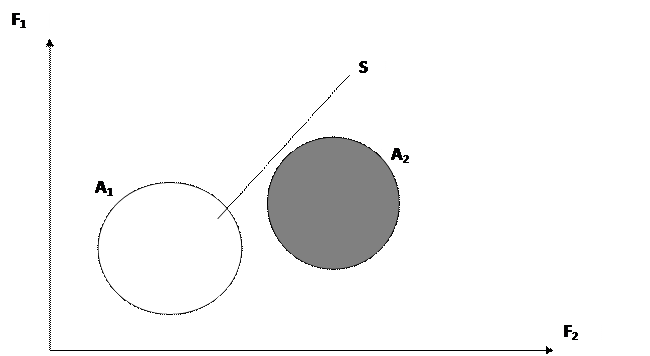
1. Непересекающиеся классы А 1, А 2 – классы, S – объект классификации
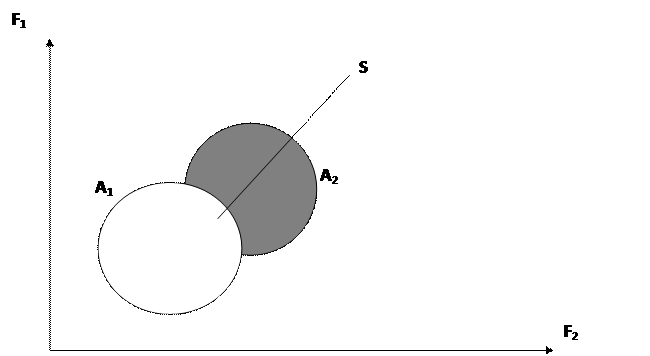
2. Пересекающиеся классы. Объект в этом случае может относиться одновременно к нескольким классам
3. Нечеткие классы. Требуется определить степень принадлежности объекта к каждому из классов. Обычно это действительное число от 0 до 1.
При дискретном рассмотрении каждый признак Fk может принимать одно значение из совокупности
F к = { F 1, F 2, …, Fk, …, Ft },
где, например F 1 – длина карандаша; F 2 – цвет; F 3 –твердость.
Каждая конкретная реализация (объект) аj задается совокупностью значений признаков:
Fk = { F 1, F 2, …, Fk, …, Ft } – класс свойств (признаков);
Nk = { N 1, N 2, …, Nl, …, Nt } – множество классов параметров.
Область распознавания можно представить следующей математической структурой:
S (A) = { A, F, N };
S (a) = { a, F (a), N (a)}.
Решение задачи распознавания образов состоит из двух этапов:
1. Обучение распознаванию по некоторому количеству эталонных образов, принадлежность которых к классу известна.
2. Распознавание, когда требуется определить, к какому классу относится представленный объект.
При обучении распознаванию можно использовать параметрический и непараметрический методы распознавания.
В параметрическом методе вид решающего правила известен и требуется определить в процессе обучения параметры этого решающего правила.
В непараметрическом методе определены вид и параметры решающего правила.
Одним из непараметрических методов является геометрический метод, предполагающий анализ расположения точек в пространстве. Обучение сводится к линейной и нелинейной деформации пространства.
Этот метод имеет следующие недостатки:
1. Геометрически можно описать ограниченное число объектов.
2. Трудно определить, к какому классу относится объект (точка S на рисунке).
К параметрическим относится Байесовский метод, использующий многомерные законы распределения вероятностей, которые имеют бесконечные интервалы.
Рассмотрим пример применения моделей распознавания образов для решения практических задачБайесовским методом.
Пусть имеется полная группа n несовместных образов, которые могут рассматриваться как объекты для распознавания. Представим их в виде неупорядоченного множества А:
А = { A 1, A 2, …, Ai, …, An }.
Известны априорные распределения вероятностей этих образов, т.е. известно, с какой вероятностью появляется данный образ:
P 1(A 1), P 2(A 2), …, Pn (An).
Если группа полная, то сумма априорных вероятностей всей группы равна единице:
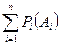 = 1
= 1
B = { B 1, B 2, …, Bj, …, Bm }.
В данном случае таким событием является появление конкретных реализаций объекта.
По теореме умножения вероятностей:
P (Bj ô Ai) = P (Bj)· P (Ai ô Bj) = P (Ai)· P (Bj ô Ai).
Отбрасывая левую часть, получаем:
P (Ai ô Bj) = P (Ai)· P (Bj ô Ai)/ P (Bj)
Выразим вероятность P (Bj) с помощью формулы для полной вероятности. Заметим, что образы Аi несовместимы, а событие-объект Bi может появиться только совместно с одним образом Ai:
Bi = A 1 Bj + A 2 Bj + … + AmBj (теоретико-множественная формула).
Так как события Ai несовместимые, то и события AiBj тоже несовместимые, поэтому
P (Bj) = 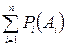 · P (Bj ô Ai).
· P (Bj ô Ai).
Выразив P (Bi), получим формулу Байеса:
P (Ai ô Bj) = 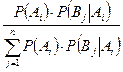 .
.
 2014-02-09
2014-02-09 4625
4625
