Расчет коэффициента Спримена. для признаков “успешность обучения” и “знание основ программирования”

для признаков “успешность обучения” и “знание основ программирования”

Студент (№ п/п)	Успешность обучения	Знание программирования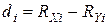
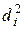
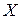
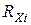
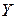
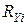
	4,88
	4,77			19,5	3,5	12,25
	4,71
	4,53			23,5	-2,5	6,25
	4,41
	4,24
	3,77
	3,76				-4
	3,65			21,5	-8,5	72,25
	3,59	10,5			-4,5	20,25
	3,59	10,5		5,5
	3,41				-2
	3,35	5,5			-4,5	20,25
	3,35	5,5		21,5	-16
	3,61			23,5	-11,5	132,25
	3,44				-1
	3,22	1,5		5,5	-4
	4,11
	3,38			3,5	3,5	12,25
	3,22	1,5			-0,5	0,25
	3,33			3,5	0,5	0,25
	3,27				-7
	3,94
	3,81			19,5	-3,5	12,25
Суммы:						1360,5

Проверка ранжирования: по каждому из признаков реальная сумма рангов, равная 300 (см. табл. 3.5), совпадет с теоретической 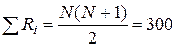и, следовательно, ранжирование проведено правильно.

Гипотезы:

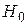- связь между успешностью обучения на МФ и знанием основ программирования отсутствует (формально: );

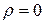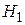- существует статистически значимая связь между успешностью обучения на МФ и знанием основ программирования (формально: ).

.

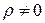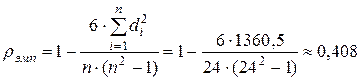Однако, наличие одинаковых (связанных) рангов в сравниваемых последовательностях наблюдени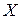й и 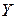означает меньшую дифференциацию свойств ранжированных признаков и приводит к завышению абсолютного значения коэффициента связи [1]. Для более точной оценки тесноты связи в расчет коэффициента Спирмена вводятся поправки:

, ,

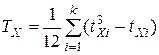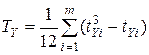где 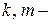число групп связанных рангов в ранжированных последовательностях признаков 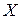и 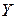соответственно;

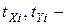число связанных рангов в 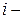ой группе для признаков 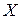и .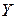

В нашем случае, в ранжированной последовательности признака 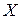имеется 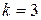групп связанных рангов по 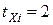ранга в каждой :

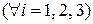1,5;	1,5;	3;	4;	5,5;	5,5;	7;	8;	9;	10,5;	10,5;	12;
13;	14;	15;	16;	17;	18;	19;	20;	21;	22;	23;	24.

Следовательно,

.

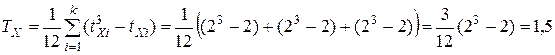В ранжированной последовательности признака 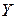всего имеется 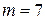групп связанных рангов (5 групп по 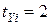ранга 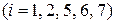и 2 группы по 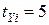рангов ):

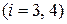1;	2;	3,5;	3,5;	5,5;	5,5;	7;	10;	10;	10;	10;	10;
15;	15;	15;	15;	15;	18;	19,5;	19,5;	21,5;	21,5;	23,5;	23,5.

Следовательно,

.

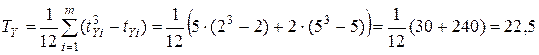Значение коэффициента Спирмена с учетом поправок на связанные ранги будет равно

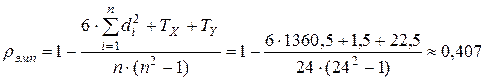
Критические значения коэффициента ранговой корреляции Спирмена 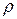в зависимости от объема выборки 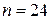и уровня значимости 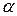равны [1, 3]:

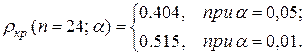
Так как 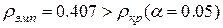, то гипотеза 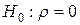(связи нет) отвергается при 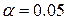, и с доверительной вероятностью 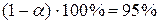может быть принята альтернативная гипотеза : .

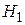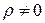Таким образом, с уверенностью 95% можно говорить о существовании прямой (т.к. 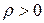) линейной связи между успешностью обучения на МФ и знанием основ программирования. Детерминация данной связи равна 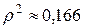, поэтому лишь на 16,6% успешность обучения на МФ зависит от одного из профильных предметов “основы программирования”, и на 83,4% от других учебных предметов, т.е. данную связь можно охарактеризовать как слабую по тесноте [1].

3.б) Для исследования корреляции между порядковым признаком “успешность обучения” и количественным признаком “уровень IQ” также можно воспользоваться коэффициентом ранговой корреляции Спирмена 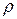[1].

Проранжируем последовательности наблюдений признаков “успешность обучения” (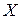) и “уровень IQ” (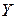) (см. табл. 3.6).

Проверка ранжирования: по каждому из признаков реальная сумма рангов, равная 300 (см. табл. 3.6), совпадет с теоретической 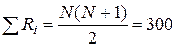и, следовательно, ранжирование проведено правильно.

Гипотезы:

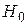- связь между успешностью обучения на МФ и уровнем интеллекта отсутствует (формально: );

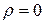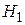- существует статистически значимая связь между успешностью обучения на МФ и уровнем интеллекта (формально: ).

.

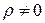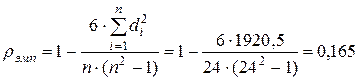Поправка на связанные ранги для признака “успешность обучения” (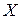) равна 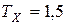(см.п. 3.а).

В ранжированной последовательности признака “уровень IQ” (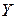) всего имеется 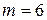групп связанных рангов (2 группы по 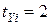ранга 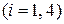и 4 группы по 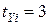ранга в каждой ):

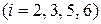1;	2,5;	2,5;	4;	6;	6;	6;	9;	9;	9;	11,5;	11,5;
14;	14;	14;	17;	17;	17;	19;	20;	21;	22;	23;	24.

Следовательно,

.

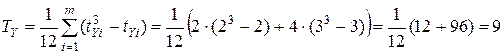Значение коэффициента Спирмена с учетом поправок на связанные ранги будет равно

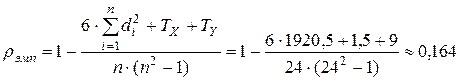
Таблица 3.6