Формы представления игр

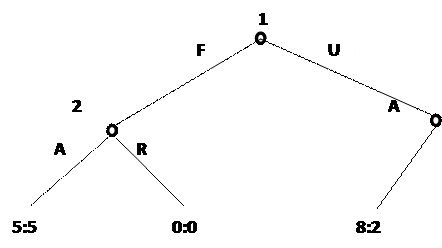
Экстенсивная форма. Игры в экстенсивной или расширенной форме представляются в виде ориентированного дерева, где каждая вершина соответствует ситуации выбора игроком своей стратегии. Каждому игроку сопоставлен целый уровень вершин. Платежи записываются внизу дерева, под каждой вершиной.

На рисунке представлена игра для двух игроков. Игрок 1 ходит первым и выбирает стратегию F или U. Игрок 2 анализирует свою позицию и решает выбрать стратегию A или R. Скорее всего первый игрок выберет U, а второй – A (для каждого из них это оптимальные стратегии); тогда они получат соответственно 8 и 2 очка.

Экстенсивная форма очень наглядна, с её помощью особенно удобно представлять игры с более чем двумя игроками и игры с последовательными ходами. Если же участники делают одновременные ходы, то соответствующие вершины либо соединяются пунктиром, либо обводятся сплошной линией.

Нормальная форма. В нормальной или стратегической форме игра описывается платёжной матрицей. Каждая сторона матрицы – это игрок, строки определяют стратегии первого игрока, а столбцы – второго. На пересечении двух стратегий можно увидеть выигрыши, которые получат игроки.

Например, н ормальная форма игры 2-х игроков, у каждого из которых по 2 стратегии, можно представить в виде матрицы.

	Игрок 2
Стратегия 1	Стратегия 2
Игрок 1	Стратегия 1	4, 3	–1, –1
Стратегия 2	0, 0	3, 4

Если игрок 1 выбирает первую стратегию, а второй игрок – вторую стратегию, то на пересечении мы видим (−1, −1), это значит, что в результате хода оба игрока потеряли по одному очку.

Игроки выбирали стратегии с максимальным для себя результатом, но проиграли, из-за незнания хода другого игрока. Обычно в нормальной форме представляются игры, в которых ходы делаются одновременно, или хотя бы полагается, что все игроки не знают о том, что делают другие участники. Такие игры с неполной информацией будут рассмотрены ниже.

Характеристическая форма. В кооперативных играх с трансферабельной полезностью, то есть возможностью передачи средств от одного игрока к другому, невозможно применять понятие индивидуальных платежей. Вместо этого используют так называемую характеристическую функцию, определяющую выигрыш каждой коалиции игроков. При этом предполагается, что выигрыш пустой коалиции равен нулю.

Если в игре с двумя сторонами образуется коалиция C, то против неё выступает коалиция N. Образуется как бы игра для двух игроков. Но так как число вариантов возможных коалиций 2 ^N (где N – количество игроков), то выигрыш для C будет некоторой характеристической величиной, зависящей от состава коалиции. Формально игра в такой форме представляется парой N, v, где N – множество всех игроков, а v: 2^N → R — это характеристическая функция.

Подобная форма представления может быть применена для всех игр, в том числе без трансферабельной полезности. В настоящее время существуют способы перевести любую игру из нормальной формы в характеристическую, но преобразование в обратную сторону возможно не во всех случаях.

Типы игр

Кооперативные и некооперативные. Игра называется кооперативной, или коалиционной, если игроки могут объединяться в группы, беря на себя некоторые обязательства перед другими игроками и координируя свои действия. Этим она отличается от некооперативных игр, в которых каждый обязан играть за себя. Развлекательные игры редко являются кооперативными, однако такие механизмы нередки в повседневной жизни.

Часто полагают, что кооперативные игры отличаются именно возможностью общения игроков друг с другом. В общем случае это неверно. Существуют игры, где коммуникация разрешена, но игроки преследуют личные цели, и наоборот.

Из двух типов игр, некооперативные описывают ситуации в мельчайших деталях и выдают более точные результаты. Кооперативные рассматривают процесс игры в целом.

Гибридные игры включают в себя элементы кооперативных и некооперативных игр. Например, игроки могут образовывать группы, но игра будет вестись в некооперативном стиле. Это значит, что каждый игрок будет преследовать интересы своей группы, вместе с тем стараясь достичь личной выгоды.

Симметричные и несимметричные. Игра будет симметричной тогда, когда соответствующие стратегии игроков равны, то есть имеют одинаковые платежи. Иначе говоря, игроки могут поменяться местами, и при этом их выигрыши за одни и те же ходы не изменятся. Многие игры для двух игроков – симметричные.

Например, в теории игр существует игра, которая называется «Дилемма заключенного». Это некооперативная игра, в которой игроки стремятся получить выгоду, сотрудничая друг с другом или предавая. Предполагается, что игрок (заключённый) максимизирует свой собственный выигрыш, не заботясь о выгоде других.

Будут ли заключенные друг друга предавать, следуя своим эгоистическим интересам, или будут молчать, тем самым минимизируя общий срок?

В дилемме заключённого предательство строго доминирует над сотрудничеством, поэтому единственное возможное равновесие – предательство обоих участников. Проще говоря, неважно, что сделает другой игрок, каждый выиграет больше, если предаст. Поскольку в любой ситуации предать выгоднее, чем сотрудничать, все рациональные игроки выберут предательство.

Ведя себя по отдельности рационально, вместе участники приходят к нерациональному решению: если оба предадут, они получат в сумме меньший выигрыш, чем если бы сотрудничали. В этом и заключается дилемма.

В повторяющейся дилемме заключённого игра происходит периодически, и каждый игрок может «наказать» другого за несотрудничество ранее. В такой игре сотрудничество может стать равновесием, а стимул предать может перевешиваться угрозой наказания.

Иногда игра, на первый взгляд может показаться симметричной из-за похожих стратегий (см. матрицу), но это не так – ведь выигрыш второго игрока при любой из стратегий (1, 1) и (2, 2) будет больше, чем у первого.

	А	Б
А	1, 2	0, 0
Б	0, 0	1, 2

С нулевой суммой и с ненулевой суммой. Игры с нулевой суммой – особая разновидность игр с постоянной суммой, то есть таких, где игроки не могут увеличить или уменьшить имеющиеся ресурсы, или фонд игры. В этом случае сумма всех выигрышей равна сумме всех проигрышей при любом ходе.

Например, матрица игры с нулевой суммой имеет следующий вид.

	А	Б
А	−1, 1	3, −3
Б	0, 0	−2, 2

В матрице числа означают платежи игрокам, и их сумма в каждой клетке равна нулю. Примерами таких игр может служить покер, где один выигрывает все ставки других; реверси, где захватываются фишки противника; либо банальное воровство.

Многие изучаемые математиками игры, в том числе уже упоминавшаяся «Дилемма заключённого», иного рода: в играх с ненулевой суммой выигрыш какого-то игрока не обязательно означает проигрыш другого, и наоборот. Исход такой игры может быть меньше или больше нуля. Такие игры могут быть преобразованы к нулевой сумме – это делается введением фиктивного игрока, который «присваивает себе» излишек или восполняет недостаток средств.

Примером игры с нулевой суммой является Антагонистическая игра. Антагонистической называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

Формально антагонистическая игра может быть представлена тройкой X, Y, F, где X и Y – множества стратегий первого и второго игроков, соответственно; F – функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий x, y (x ∈ X; y ∈ Y), действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.

Исторически антагонистические игры являются первым классом математических моделей теории игр, при помощи которых описывались азартные игры. Считается, что благодаря этому предмету исследования теория игр и получила свое название. В настоящее время антагонистические игры рассматриваются как часть более широкого класса некооперативных игр.

Простейшим примером антагонистической игры является игра "Орлянка". Первый игрок прячет монету орлом или решкой вверх, а второй пытается угадать, как она спрятана. Если он не угадывает - он платит первому одну денежную единицу, если угадывает - первый платит ему одну денежную единицу.

X \ Y	Орел	Решка
Орел	–1, 1	1, –1
Решка	1, –1	–1, 1

В данной игре каждый участник имеет две стратегии: "орел" и "решка". Множество ситуаций в игре состоит из четырех элементов. В строках таблицы указаны стратегии х первого игрока Х, в столбцах – стратегии y второго игрока Y. Для каждой из ситуаций указаны выигрыши первого и второго игроков.

В аналитическом виде функция выигрыша первого игрока имеет следующую форму:

1, при x ≠ y

F₁ (x, y) =

–1, при x = y

где x ∈ X и y ∈ Y – стратегии первого и второго игроков, соответственно.

Так как выигрыш первого игрока равен проигрышу второго, то F ₂(x, y) = − F ₁(x, y).

Игрой с отличной от нуля суммой является торговля, где каждый участник извлекает выгоду. Сюда также относятся шашки и шахматы; в которых игрок может превратить свою рядовую фигуру в более сильную, получив преимущество. Во всех этих случаях сумма игры увеличивается. Широко известным примером, где она уменьшается, является война.

Параллельные и последовательные. В параллельных играх игроки ходят одновременно, или, по крайней мере, они не осведомлены о выборе других до тех пор, пока все не сделают свой ход. В последовательных, или динамических, играх участники могут делать ходы в заранее установленном либо случайном порядке, но при этом они получают некоторую информацию о предшествующих действиях других. Эта информация может быть даже не совсем полной, например, игрок может узнать, что его противник из десяти своих стратегий точно не выбрал пятую, ничего не узнав о других.

Параллельные игры обычно представляют в нормальной форме, а последовательные – в экстенсивной.

С полной или неполной информацией. Важное подмножество последовательных игр составляют игры с полной информацией. В такой игре участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников, что позволяет им в некоторой степени предсказать последующее развитие игры. Полная информация не доступна в параллельных играх, так как в них неизвестны текущие ходы противников. Большинство изучаемых в математике игр – с неполной информацией. Например, игры Дилемма заключённого или Сравнение монеток – это игры с неполной информацией. В то же время есть интересные примеры игр с полной информацией: например шахматы, шашки, го и другие.

Часто понятие полной информации путают с похожим понятием совершенной информации, для которого достаточно лишь знание всех доступных противникам стратегий, знание всех их ходов необязательно.

Игры с бесконечным числом шагов. Игры в реальном мире или изучаемые в экономике игры, как правило, длятся конечное число ходов. В математике, и в частности, в теории множеств рассматриваются игры, способные продолжаться бесконечно долго. Причём победитель и его выигрыш не определены до окончания всех ходов.

Задача, которая обычно ставится в этом случае, состоит не в поиске оптимального решения, а в поиске хотя бы выигрышной стратегии. Иногда даже для игр с полной информацией и двумя исходами – «выиграл» или «проиграл» – ни один из игроков не имеет такой стратегии.

Дискретные и непрерывные игры. Большинство изучаемых игр дискретны: в них конечное число игроков, ходов, событий, исходов и т.п. Однако эти составляющие могут быть расширены на множество вещественных чисел. Игры, включающие такие элементы, называются дифференциальными. Они связаны с какой-то вещественной шкалой (обычно – шкалой времени), хотя происходящие в них события могут быть дискретными по природе. Дифференциальные игры также рассматриваются в теории оптимизации, находят своё применение в технике и технологии, физике.

Метаигры. Это такие игры, результатом которых является набор правил для другой игры (называемой целевой или игрой-объектом). Цель метаигр – увеличить полезность выдаваемого набора правил. Теория метаигр связана с теорией оптимальных механизмов.

Дифференциальные игры. В теории управления при изучении управления объектом в конфликтных ситуациях, рассматриваются дифференциальные игры, в которых возможности игроков описываются дифференциальными уравнениями, содержащими управляющие векторы, которыми распоряжаются игроки. Для выбора своего управления каждый игрок может использовать лишь текущую информацию о поведении игроков. Различают дифференциальные игры двух игроков и многих игроков.

Наиболее исследованными являются Дифференциальные игры преследования, в которых количество игроков равно 2, одного называют догоняющим, другого убегающим. Цель догоняющего – приведение вектора z (t) на заданное множество М за возможно короткое время; цель убегающего – по возможности оттянуть момент прихода вектора z (t) на множество M.

Методика определения стратегий для игры двух лиц с нулевой суммой на примере "игры полковника Блотто"

Распределение сил для занятия позиций:

Ø число позиций – 2;

Ø число полков у полковника Блотто – 4;

Ø число полков у противника – 3.

Правила определения платежей:

§ если на позиции у полковника полков больше, чем у противника, то он получает все полки противника и плюс один полк, так как занятие позиции эквивалентно захвату одного полка;

§ если на данной позиции у полковника полков меньше, то он теряет свои полки на данной позиции и плюс позицию, то есть еще один полк;

§ общий платеж равен сумме платежей на обеих позициях.

У полковника Блотто есть пять стратегий, у противника – четыре стратегии по распределению полков на двух позициях. Распределение платежей в зависимости от выбранной стратегии заносится в платежную матрицу

		b1	b2	b3	b4
		3,0	0,3	2,1	1,2
a1	4,0	4,0	1,–1	3,–1	2,–1
a2	0,4	–1,1	0,4	–1,2	–1,3
a3	3,1	0,1	1,–2	3,0	2,–2
a4	1,3	–2,1	1,0	–2,2	0,3
a5	2,2	–3,1	1,–3	0,2	2,0

Суммарная платежная матрица имеет вид:

min выигрыш А		b1	b2	b3	b4
		3,0	0,3	2,1	1,2
a1	4,0
a2	0,4
a3	3,1		–1			–1
a4	1,3	–1				–1
a5	2,2	–2	–2			–2
max проигрыш В

Оптимальный выбор стратегии для А – наибольший из минимальных выигрышей – max из min – 0, 0 (a ₁, a ₂).

Оптимальный выбор стратегии для В – наименьший из максимальных проигрышей – min из max – 3, 3 (b ₃, b ₄).

Обычно при выборе стратегии руководствуются одним из принципов: осторожности (минимакса) Гурвица или Сэвиджа.

Математические модели теории игр с полной информацией. Принцип осторожности

Модель игры может быть представлена в матричной форме в виде суммарной платежной матрицы

	Наименьший выигрыш Аi

	B1	B2	B3	B4
А1
А2
А3
Наибольший проигрыш Вj

min max

Сторона А имеет три стратегии (А ₁, А ₂, А ₃). Сторона В – четыре стратегии (В ₁, В ₂, В ₃, В ₄).

Получаем две границы игры:

a – max min c_ij = 10 – максимальный выигрыш

j i

b – min max c_ij = 10 – минимальный проигрыш