3.
.
Пусть прямая l проходит через две данные точки и. Составим каноническое уравнение прямой, проходящей через эти точки. Для этого найдем направляющий вектор, за который примем вектор
2.
Y
1.
Прямая линия в пространстве
Учебные и воспитательные цели: знать основные виды уравнений прямой в пространстве, условия параллельности и перпендикулярности
Учебные вопросы занятия:
1. Виды уравнения прямой: векторное, параметрическое и каноническое уравнение прямой в пространстве. – 15 мин.
2. Уравнение прямой в пространстве, проходящей через две данные точки. - 10 мин.
3. Прямая как линия пересечения двух плоскостей. –15 мин.
4. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности. –15 мин.
5. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых в пространстве. – 10 мин.
6. Точка пересечения прямой и плоскости. – 15 ми
Положение прямой в пространстве определено, если на прямой линии задана точка 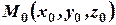 и вектор
и вектор 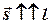 параллельный прямой или лежащий на ней. Вектор
параллельный прямой или лежащий на ней. Вектор 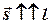 называется направляющим вектором этой прямой. Задать вектор, значит задать его координаты, т.е. проекции на оси координат. Направляющий вектор задается координатами:
называется направляющим вектором этой прямой. Задать вектор, значит задать его координаты, т.е. проекции на оси координат. Направляющий вектор задается координатами: 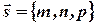 .
.
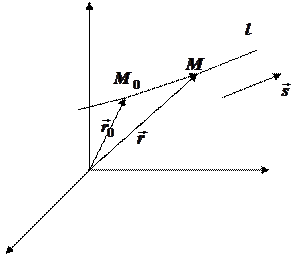 Z
Z
Возьмем произвольную точку 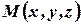 на прямой
на прямой 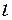 . Вектор
. Вектор 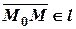 коллинеарен направляющему вектору
коллинеарен направляющему вектору 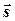 , поэтому
, поэтому
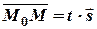 (1)
(1)
где скалярный множитель t называется параметром и может принимать любое значение в зависимости от положения точки М на прямой.
Проведем радиус векторы к точкам 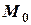 и М:
и М:
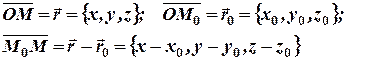 (2)
(2)
Тогда с учетом полученных равенств (2) перепишем (1) в виде:
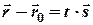 . (3)
. (3)
Уравнение (3) называется векторным уравнением прямой. Оно показывает, что каждому значению параметра соответствует радиус вектор некоторой точки, лежащей на прямой.
Представим уравнение (3) в координатной форме:
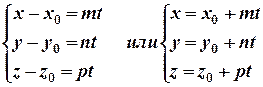 . (4)
. (4)
Уравнение (4) называется параметрическим уравнением прямой. При изменении параметра 
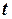 изменяются координаты,
изменяются координаты, 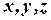 и точка
и точка 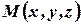 движется по прямой. Из уравнения (4) можно найти параметр
движется по прямой. Из уравнения (4) можно найти параметр 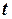 :
:
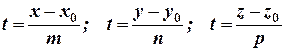 (5)
(5)
Приравнивая правые части равенств (5) получим
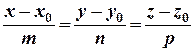 (6)
(6)
Уравнение (6) называется каноническим уравнением прямой линии в пространстве.
Заметим, что уравнение (6) называется уравнением прямой, проходящей через точку 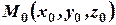 с направляющим вектором
с направляющим вектором 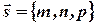 . В случае, когда направляющим вектором является единичный вектор
. В случае, когда направляющим вектором является единичный вектор
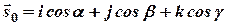
уравнение (5) имеет следующий вид: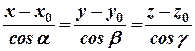 .
.
Тогда 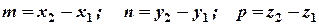 .
.
Используя каноническое уравнение прямой, и, рассматривая ее как прямую, проходящую через точку 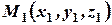 , получим
, получим
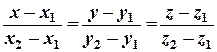 . (7)
. (7)
Уравнение (7) называется уравнением прямой, проходящей через две данные точки.
Пусть даны две плоскости
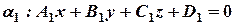
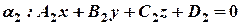 ,
,
причем они не параллельны: 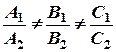 . Тогда l можно рассматривать как линию пересечения двух плоскостей
. Тогда l можно рассматривать как линию пересечения двух плоскостей 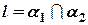 , т.е.
, т.е.
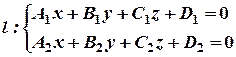 (8)
(8)
Уравнения (8) называется общими уравнениями прямой линии в пространстве.
Так как прямая 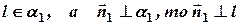 , аналогично
, аналогично
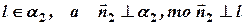 .
.
Тогда за вектор 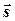 естественно принять
естественно принять 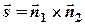 . Следовательно, координаты направляющего вектора найдем по формуле
. Следовательно, координаты направляющего вектора найдем по формуле
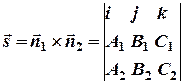
За точку 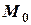 на прямой можно выбрать любую точку, координаты которой удовлетворяют общим уравнениям прямой, т.е. являются решениями системы уравнений (8). Но так как уравнений два, а неизвестных три, то такая система имеет бесчисленное множество решений. Тогда одна из неизвестных принимается за параметр или приравнивается к нулю, и находятся две другие координаты точки прямой.
на прямой можно выбрать любую точку, координаты которой удовлетворяют общим уравнениям прямой, т.е. являются решениями системы уравнений (8). Но так как уравнений два, а неизвестных три, то такая система имеет бесчисленное множество решений. Тогда одна из неизвестных принимается за параметр или приравнивается к нулю, и находятся две другие координаты точки прямой.
Замечание: возможен обратный переход. Пусть
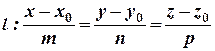 . Отсюда
. Отсюда 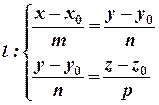 - общие уравнения прямой.
- общие уравнения прямой.
 2014-02-09
2014-02-09 1804
1804