Уравнение (3) называется уравнением прямой в отрезках

2.

1.

Для получения общего уравнения прямой на плоскости вспомним уравнение плоскости .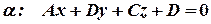

Найдем линию пересечения плоскости с одной из координатных плоскостей, например, плоскостью 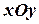. Для этого решим систему уравнений

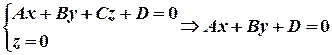(1)

Что будет являться линией пересечения? (Ответ: Линией пересечения будет прямая, заданная уравнением (1).)Что характерно для этого уравнения? Уравнение (1) первой степени относительно текущих координат 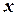и 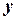. Верно и обратное утверждение: всякое уравнение первой степени относительно координат определяет прямую.

Координаты любой точки, лежащей на прямой, удовлетворяют уравнению прямой.

Уравнение вида (1) называется общим уравнением прямой на плоскости 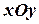. Аналогично можно получить уравнения прямой в координатных плоскостях 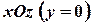, получим 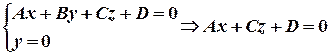и

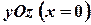, т.е. .

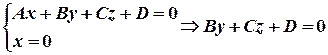Исследуем уравнение прямой (1). Если вы проработали предыдущую лекцию, то вам будет все хорошо понятно. Итак, дано уравнение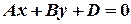

1) Пусть 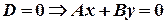. Отсюда 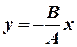. Что можно сказать относительно этой прямой? Вспомните прямую 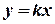. (Проходит через начало координат и расположение зависит от знака 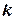, см. рисунок 1).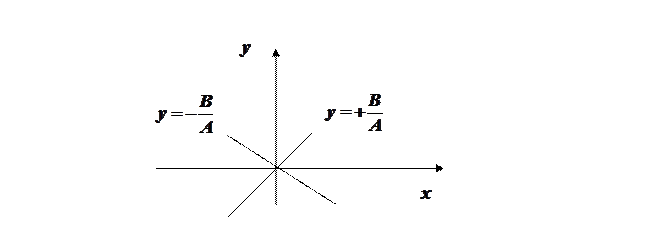

Рисунок 1.

2) Пусть 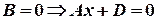. Тогда 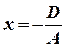=const. Что можно сказать об этой прямой? (Параллельна оси 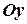,см Рис.2.).

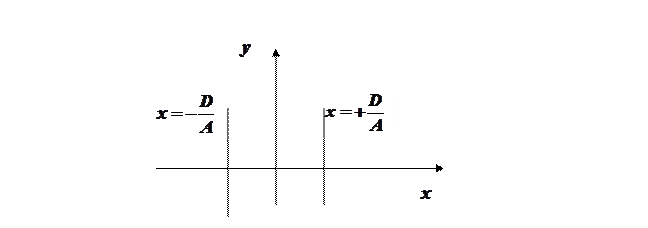
Рисунок 2.

Это прямые простые, но вы должны уметь их строить.

3) Пусть 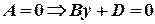. Тогда 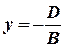=const. Что можно сказать об этой прямой? (Параллельна оси 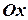,см. Рис. 3.).

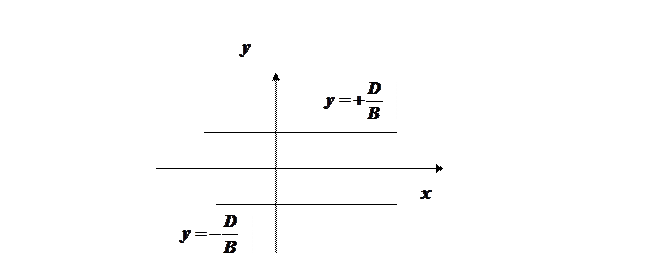
Рисунок 3.

4) Пусть 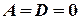, тогда получим 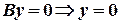. Это уравнение какой прямой? -(Курсант - уравнение оси абсцисс 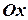). Итак: : .

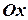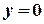5) Пусть 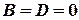, тогда получим 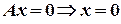. Это уравнение какой прямой? -(Курсант - уравнение оси ординат 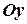). Итак: : .

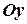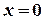Пусть дано общее уравнение прямой (1) 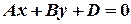. Преобразуем его следующим образом:

.

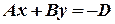Разделим обе части равенства на (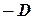), получим:

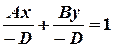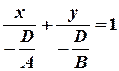или . (2)

Введем обозначения 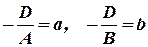, тогда уравнение (2) перепишется в виде 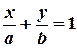. (3)

Его можно было получить иначе, используя уравнение плоскости в отрезках. Пусть дана плоскость в виде уравнения в отрезках:

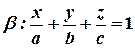(4).

Найдем линию пересечения плоскости 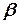с координатной плоскостью 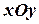, получим: 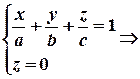уравнение примет вид .

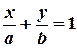В уравнении (3) величины 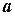и 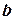показывают какие отрезки отсекает прямая на осях координат (см. рис. 4.).

Рисунок 4.

Аналогично можно получить уравнения прямой в других координатных плоскостях.