6.
5.
4.
Пусть дана прямая 
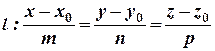 и плоскость
и плоскость
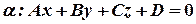
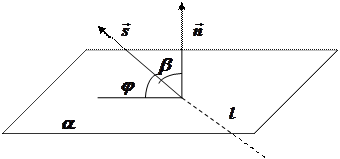
Искомый угол 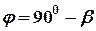 . Из скалярного произведения векторов имеем
. Из скалярного произведения векторов имеем
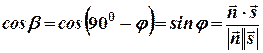 .
.
Таким образом, угол между прямой и плоскостью находится по формуле
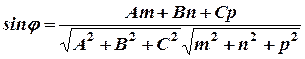 . (9)
. (9)
Условие параллельности прямой и плоскости: 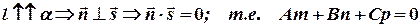 .
.
Условие перпендикулярности прямой и плоскости:
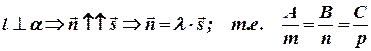 .
.
Под углом между прямыми в пространстве понимается угол между их направляющими векторами.
Пусть в пространстве даны две прямые:
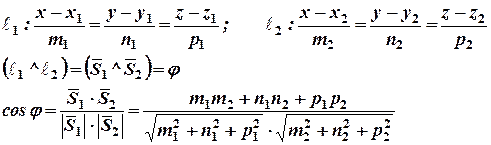
Условие параллельности
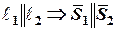 т.е.
т.е. 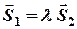 или
или 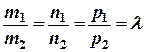
Условие перпендикулярности
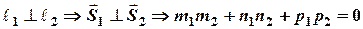
Пусть требуется найти точку пересечения прямой
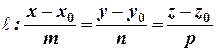
с плоскостью 
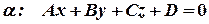
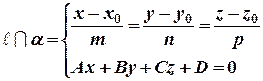
Запишем уравнение прямой линии в параметрическом виде:
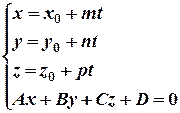
и решим систему методом подстановки, получим:
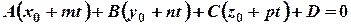
Найдем параметр 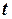
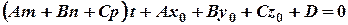
1) Если 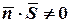 т.е.
т.е. 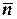 не
не 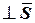 , то
, то 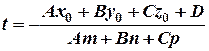 . Подставив в параметрическое уравнение прямой
. Подставив в параметрическое уравнение прямой 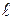 полученное значение параметра определим точку
полученное значение параметра определим точку 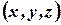 в которой
в которой 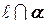 .
.
2) 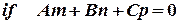 , а правая часть
, а правая часть 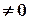 тогда
тогда 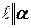 .
.
3) 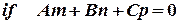 и правая часть
и правая часть 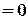 , то
, то 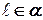
Учебные и воспитательные цели: знать основные уравнения прямой на плоскости
Учебные вопросы занятия:
1. Общее уравнение прямой и его исследование – 15 мин.
2. Уравнение прямой в отрезках - 15 мин.
3. Уравнение прямой с угловым коэффициентом –15 мин.
4. Уравнение прямой, проходящей через данную точку в заданном направлении –15 мин.
5. Уравнение прямой, проходящей через две данные точки - 10 мин.
6. Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности. – 10 мин.
 2014-02-09
2014-02-09 720
720








