5.
4.
3.
Положение прямой на плоскости вполне определяется заданием угла 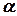 , образованного прямой с положительным направлением оси абсцисс, и величиной отрезка
, образованного прямой с положительным направлением оси абсцисс, и величиной отрезка 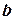 , отсекаемым от оси
, отсекаемым от оси 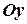 . Значит прямая на плоскости имеет два параметра
. Значит прямая на плоскости имеет два параметра 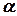 и
и 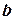 . Направление отсчета угла идет против часовой стрелки.
. Направление отсчета угла идет против часовой стрелки.
Величина 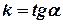 называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой.
Какая же перед нами стоит задача? Найти уравнение прямой 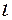 по известным
по известным 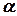 и
и 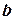 .
.
Для решения поставленной задачи через точку пересечения прямой 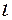 с осью
с осью 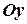 проведем прямую параллельную оси абсцисс (см. рис. 5)
проведем прямую параллельную оси абсцисс (см. рис. 5)
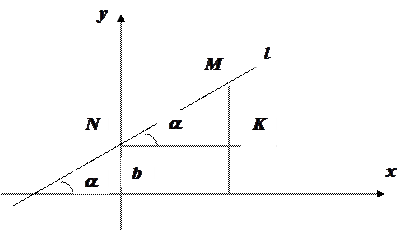
Рис.5
На прямой 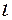 возьмем произвольную точку
возьмем произвольную точку 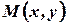 и опустим из нее перпендикуляр на ось абсцисс. Из полученного треугольника
и опустим из нее перпендикуляр на ось абсцисс. Из полученного треугольника 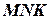 найдем по определению
найдем по определению 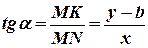 . Отсюда получим уравнение вида
. Отсюда получим уравнение вида 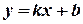 (5)
(5)
Уравнение (5) называется уравнением прямой с угловым коэффициентом.
Пусть прямая проходит через точку 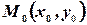 . По условию задано направление. Что это значит? (Известен угловой коэффициент
. По условию задано направление. Что это значит? (Известен угловой коэффициент 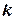 ). Требуется найти уравнение прямой
). Требуется найти уравнение прямой 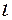 .
.
Какое уравнение использовать из уже известных? (Будем искать уравнение в виде 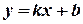 ).
).
Так как точка 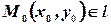 , то её координаты удовлетворяют уравнению прямой
, то её координаты удовлетворяют уравнению прямой
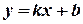 . (5)
. (5)
Тогда получим, 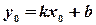 . (6)
. (6)
Вычтем из уравнения (5) уравнение (6), получим 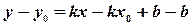
или 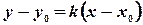 . (7)
. (7)
Уравнение (7) называется уравнением прямой, проходящей через данную точку в заданном направлении.
Пусть прямая 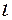 проходит через две точки
проходит через две точки 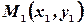 и
и 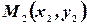 , тогда координаты этих точек удовлетворяют уравнению прямой
, тогда координаты этих точек удовлетворяют уравнению прямой 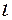 . Используем уравнение вида (7). Получим:
. Используем уравнение вида (7). Получим:
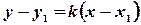 (8)
(8)
Так как прямая, заданная уравнением (8) будет проходить и через точку 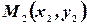 , то координаты этой точки будут удовлетворять уравнению (8), т.е.
, то координаты этой точки будут удовлетворять уравнению (8), т.е.
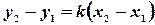 . (9)
. (9)
Разделим уравнение (8) на уравнение (9), получим
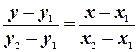 . (10)
. (10)
таким образом путем деления уравнений мы избавились от углового коэффициента 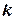 , который нам не был известен.
, который нам не был известен.
Однако часто на практике проще решается задача, если найден угловой коэффициент прямой, проходящей через две данные точки и нет необходимости находить само уравнение прямой. Его легко найти из уравнения (9):
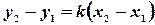 .
.
Отсюда 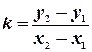 .
.
 2014-02-09
2014-02-09 406
406







