Примеры неравновесных процессов

1. Теплообмен. Рассмотрим простейший пример: теплообмен между двумя телами с одинаковой теплоемкостью С и начальными температурами Т₁ и Т₂. Из уравнения теплового баланса следует, что в результате теплообмена оба тела достигнут одинаковой температуры Т_К =1/2(T₁+T₂). При этом согласно (31) изменение энтропии системы будет положительным:

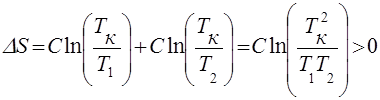(36)

(аргумент логарифма больше единицы, так как среднее арифметическое больше среднего геометрического).

2. Расширение идеального газа в пустоту. Внутренняя энергия и, следовательно, температура идеального газа при расширении его в пустоту остаются постоянными. Изменение энтропии находим из формулы (32):

S₂ –S₁ =nRln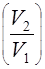 (37)

Возрастание энтропии при адиабатическом расширении в пустоту (увеличении V при постоянной U} можно доказать для любой простой системы. Если рассматривать S в (23) как функцию переменных (U, V), то получим 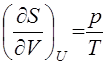>0

3. Смешение газов. Рассмотрим теплоизолированный сосуд, разделенный перегородкой на две равные части, в каждой из которых содержится по одному молю идеального газа при одинаковых температурах и давлениях. При убирании перегородки газы смешиваются; из формулы (37) следует, что энтропия системы увеличивается на 2Rln2 (энтропия смешения). В случае различных газов начальное состояние отличается от конечного; газы можно снова разделить, совершая работу над специальными поршнями, пропускающими молекулы только одного сорта. Однако для одинаковых газов начальное и конечное состояния системы тождественны, и энтропия не должна меняться. Отсутствие непрерывного перехода от почти одинаковых к полностью тождественным молекулам называют парадоксом Гиббса.

Статистический смысл энтропии. Формула Больцмана

S=klnW (38)

(k — постоянная Больцмана) связывает энтропию макроскопического состояния со статистическим весом этого состояния, т. е. числом различных микроскопических состояний, которые его реализуют. Чем больше W, тем больше вероятность состояния; при неравновесных процессах система переходит от менее вероятных к более вероятным состояниям. Логарифм обеспечивает аддитивность энтропии: статистический вес системы, состоящей из двух независимых подсистем, равен произведению их статистических весов.

Чтобы проиллюстрировать формулу (36), вычислим пространственную часть энтропии газа. Разобьем объем на маленькие ячейки объемом v. Каждая молекула может быть помещена в любую из V/v ячеек, т. е. число независимых состояний равно W = (V/v)^N, где N — число молекул газа. Для энтропии получим S = klnW = kNln(V/v) = n Rln(V/v). Квантовая статистика утверждает, что одинаковые частицы принципиально неразличимы, т. е. W надо разделить на число перестановок между ними N!. В результате для пространственной части энтропии получим выражение S=kNln(V/Nv). Нетрудно убедиться, что таким образом удается разрешить парадокс Гиббса.

Третье начало термодинамики. Третье начало термодинамики (теорема Нернста) утверждает, что при приближении температуры к абсолютному нулю энтропия любой системы стремится к определенному конечному значению, не зависящему от значения остальных термодинамических параметров. Энтропию системы при Т = 0 принимают равной нулю. Статистическое объяснение: при Т = 0 система находится в наинизшем энергетическом состоянии, кратность которого (равная статистическому весу системы W при Т = 0) невелика, и в соответствии с формулой Больцмана (36) энтропия пренебрежимо мала. Следствия третьего начала: при Т 0 теплоемкости С_V и С_p системы, а также ее температурные коэффициенты объемного расширения a и давления b стремятся к нулю.

Система в термостате. Свободная энергия. Рассмотрим изменение состояния системы, находящейся в тепловом контакте с термостатом, имеющим постоянную температуру Т. Такую же температуру будет иметь сама система в начальном и конечном равновесных состояниях. Неравенство (34) после «цепочки» преобразований Q/T £ S₂ -S₁ Þ (U₂–U₁)+A £ TS₂ –TS₁ Þ U₁ –TS₁ - (U₂-TS₂) ³ A принимает вид:

Y₁-Y₂ ³ A,(39)

где Y = U — TS — новая функция состояния, называемая свободной энергией. Если объем системы не меняется, то в рассматриваемом неравновесном процессе

Y₂ £ Y₁,

т.е. свободная энергия не возрастает. Другими словами, равновесное состояние системы постоянного объема, находящейся в тепловом контакте с термостатом, соответствует минимуму свободной энергии. Для равновесного процесса неравенство в этих уравнениях превращается в равенство. Из формулы (30) следует, что

dY = -SdT — pdV (40)

Поэтому естественными переменными для свободной энергии являются объем и температура: Y = Y(V, Т).

Если система в термостате находится в механическом контакте (легкий поршень, гибкая оболочка) с внешней средой, имеющей фиксированное давление р (такое же давление будет у самой системы в равновесном состоянии), то работа против внешних сил равна А = p(V₂ — V₁). Из (39) получим

Y₁+рV₁ ³ Y₂+рV₂или Ф₁ ³ Ф (32)

где Ф = Ф + pV = U — TS + pV — термодинамический потенциал Гиббса (при обратимом процессе Ф = const). Равновесному состоянию для системы в термостате и гибкой оболочке соответствует минимум Ф(р,Т). Так как dФ = —SdT + V dp, то естественными переменными для термодинамического потенциала являются давление и температура: Ф = Ф(р, Т). При постоянных давлении и температуре термодинамический потенциал пропорционален количеству вещества: Ф(р, Т, m) = тф (ф — удельный термодинамический потенциал) или Ф(р, Т, N) = N×m (m —термодинамический потенциал в расчете на одну частицу, или химический потенциал).

Канонические уравнения состояния. Естественные переменные. Хотя функции U, I, S, Y, Ф могут рассматриваться в любых независимых переменных, для каждой из них существуют естественные переменные. Для энтропии это переменные (U, V), для энтальпии — (U, р), для свободной энергии — (V, Т), для потенциала Гиббса— (р, Т). Функция в естественных переменных называется каноническим уравнением состояния. Зная любое каноническое уравнение, можно получить как термическое, так и калорическое уравнения состояния. Например, - 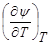дает выражение для p(V, Т), а выразив S(V, Т) = - 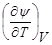, найдем U(V, Т) =Y + TS.