О1 / р \Ор J Т

О2

OV /Т

U/l КI

Интегрируя, приходим к барометрической формуле.

Распределение Максвелла — Больцмана. Оба распределения — Максвелла (45) и Больцмана (46) — содержат выражение exp(—£/kT). Распределение Максвелла — Вольцмана выражает вероятность того, что произвольная молекула из сосуда, содержащего N молекул, находится в области пространства (ж, x+dx; у, y+dy; z, z+dz) и имеет скорость в интервале («г, v_x + dv_x; v_y, v_y+dv_y; v_z, v_z + dv_z):

dN dn(r)d³r пМФМ,₃,₃ . / e \.3.3 ,»~\
—— = -^—— = ^J-^-d³rd³v = A_exp(—^)d³rd³v. (47)

Здесь d³r = dx dy dz, d³v = dv_x dv_y dv_z, e — -m₀v² + £_n(r) — меха-

2t

ническая энергия молекулы, А — коэффициент, который можно найти из условия нормировки. Общее распределение Максвелла — Больцмана применимо к любым видам энергии молекулы: энергии вращения, энергии колебаний, потенциальной энергии, зависящей от ориентации молекул, и т. д.

2.6. Реальные газы. Уравнение Ван-дер-Ваальса

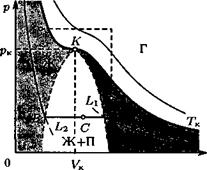
Изотермы реального газа. Если температура газа меньше критической (см. ниже), то при равновесном изотермическом уменьшении его объема наблюдаются следующие процессы (рис. 21):

1. До точки А давление возрастает. Если температура далека от критической, то вплоть до точки А хорошо выполняется уравнение

состояния идеального газа.

V

Рис. 21

изотерм АЬ\ и L^B соответствуют метастабилъным состояниям, т. е. состояниям, в которых система может существовать некоторое время, но потом быстро переходит в устойчивое состояние на линии АВ. (Имея в виду процессы при постоянном давлении или объеме, их называют переохлажденным паром или перегретой жидкостью.) Существование метастабильных состояний объясняется тем, что образование маленьких зародышей новой фазы (жидкости в паре или пара в жидкости) невыгодно из-за поверхностной энергии (см. разд. 2.8). 3. После точки В давление резко возрастает. В сосуде находится только жидкость. Чем выше температура, тем короче горизонтальный участок изотермы. Наконец, при критической температуре Тк от горизонтального участка остается только точка перегиба К (рис.21). Давление в этой критической точке называют критическим давлением рк, а объем одного моля газа в этом состоянии — критическим объемом VK. При Т > Тк изотерма представляет собой плавную монотонную функцию.

1. На участке АВ давление в системе не меняется. В сосуде появляется жидкость, отделенная от газа четкой границей (поверхностью раздела). Газ, находящийся в равновесии с жидкостью, называют насыщенным паром. Отношение масс жидкости и пара в произвольной точке равно отношению горизонтальных отрезков, на которые эта точка делит отрезок АВ: т_ж/т_п = АС/СВ. Участки

Область выше критической изотермы называют (истинным) газом (его нельзя изотермически перевести в состояние «жидкость + пар»), а область под критической изотермой делится на три: жидкость, ненасыщенный пар и жидкость + насыщенный пар. Из области «П» в область «Ж» можно перейти плавно, обойдя область «П + Ж», т. е. газ и жидкость отличаются только количественными показателями.

Уравнение Ван-дер-Ваальса для одного моля идеального газа имеет вид

/ \

(48)

(Уравнение (3) из разд. 1.1 для v молей получается подстановкой У_д = У/f.) Постоянная 6 учитывает уменьшение свободного объема для движения молекул за счет их собственного объема; считается, что эта константа равна учетверенному объему всех молекул:

6 = 47VA • дТг^³. Член о/Уд учитывает уменьшение давления за счет взаимного притяжения молекул; это особенно ясно видно из выражения для внутренней энергии газа Ван-дер-Ваальса: U = С^уТ ~ о/У^-

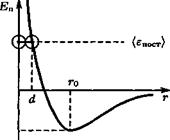
Среднее взаимодействие между молекулами описывают модельным выражением для потенциальной энергии, содержащим два члена: первый соответствует сильному отталкиванию на малых расстояниях (~ 10~¹⁰ м), второй — ван-дер-ваальсовским силам притяжения на больших расстояниях (рис. 22):

Минимум Е_П соответствует среднему расстоянию между молекулами в отсутствие теплового движения. При kT <C Е_т\п движение молекул сводится к колебаниям возле дна ямы (твердое тело), случай kT ~ Е_т-,„ соответствует жидкому состоянию, а случай kT» Е_т-,_п — газообразному. Ввиду крутого наклона левой ветви кривой, соответствующей отталкиванию молекул, положение точки поворота при сближении молекул газа слабо зависит от их средней энергии (см. также разд. 1.5).

Изотермы газа Ван-дер-Ваальса. Вычисление критических параметров. На рис. 23 изображены изотермы газа, описываемого уравнением (48). На участке K\Ki не выполняется условие

механической устойчивости (-^) ^ О, переход между правой и ле-

вой ветвями происходит по горизонтальному участку АВ. Правило Максвелла: положение отрезка АВ определяется условием равенства заштрихованных площадей. (В противном случае изотермический цикл AK\KiBA производил бы работу, что противоречит второму началу термодинамики.) Участки АК\ и К%В соответствуют метастабильным состояниям.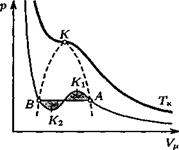

rnin

Рис. 22

Рис. 23

В критической точке выполняются сразу два условия:

dV2

= 0. Выразив р из (48) и подставив в эти уравнения, найдем:

VK =,

1 a

8 а

276/Г

—____ Т —
_к — -_ ₂, -* к —.

Критические параметры удовлетворяют соотношению: р_кУ_к — -RT_K.

Если ввести относительные переменные v = V/V_K, it = р/р_к и в = Т/Т_К, то (48) принимает вид:

1 _₂ _ 8

3 ^V 3 '

единый для всех газов. Следовательно, уравнение Ван-дер-Ваальса удовлетворяет экспериментально установленному принципу соответственных состояний, который утверждает, что если две относительные переменные двух газов совпадают, то совпадает и третья. Этот закон хорошо выполняется для большинства газов.

2.7. Равновесие фаз. Фазовые переходы

Условия равновесия фаз. Фазой называется часть системы, однородная по физическим и химическим свойствам. Одно и то же по химическому составу вещество может находиться в разных фазах. Примерами двухфазной системы являются: (жидкость+насыщенный пар), (твердое тело+жидкость) и (твердое тело+пар).

Условия равновесия фаз: 1) равенство давлений — механическое равновесие; 2) равенство температур — тепловое равновесие; 3) равенство химических потенциалов (или удельных потенциалов Гиббса) — равновесие по отношению к переходу вещества из одной фазы в другую. Последнее условие соответствует минимуму термодинамического потенциала Гиббса Ф — ц\М\ + p,?.(N — ni) (см. разд. 2.4) по отношению к числу частиц в одной из фаз ni. Условие fii(p,T) = fj,₂(p,T) дает (для простой системы) уравнение для кривой сосуществования фаз р(Т); двухфазная простая система имеет только одну степень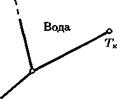свободы. Так, давление насыщенного пара (положение горизонтального участка изотермы, см. разд. 2.6) является однозначной функцией температуры (кривая парообразования); то же самое относится к зависимости температуры плавления от внешнего давления (кривая плавления) и к зависимости от температуры давления пара над твердой поверхностью (кривая возгонки).

Пар

На рис. 24 приведены все три кривые — парообразования (I), плавления (II) и возгонки (III) — для воды. Точка пересечения этих кривыхназывается тройной точкой (для воды *₃ = 0,01°С, рз = 610,5 Па). _Рис. 24Для существования трехфазной системы должны выполняться сразу два условия: (i_n(p, Т) = ц_ж(р, Т) и р_ж(р,Т) = Д1_тв(р, Т), которые однозначно определяют ее давлениеи температуру.

Фазовый переход первого рода. Теплота и энтропия перехода. Чтобы в двухфазной системе перевести часть вещества массой m из одной фазы в другую, не меняя при этом давления и температуры, надо сообщить системе теплоту Q = mq, которую называют (скрытой) теплотой фазового перехода (q — удельная теплота перехода). При переходе вещества в новую фазу ее энтропия изменяется на AS = Q/T = mq/T, а внутренняя энергия на AU — mq — mpAv (и = V/m — удельный объем). Величину As — q/T называют удельной энтропией перехода, а Аи = q — pAv — изменением удельной внутренней энергии при переходе. Переход вещества между фазами двухфазной системы, связанный с поглощением (выделением) теплоты перехода и сопровождающийся скачкообразным изменением внутренней энергии, энтропии, плотности (объема) и др., называется фазовым переходом первого рода. (Название связано с тем, что скачок испытывают величины, являющиеся первыми производными термодинамического потенциала Гиббса: S =—(-^=} и V =(-£-).)

Уравнение Клапейрона — Клаузиуса. Если изменить температуру двухфазной системы, то ее давление изменится таким образом, что химические потенциалы (или удельные потенциалы Гиббса) фаз останутся равными: <1ф\ = d<j>2, или —si dT + Vi dp = — $2 dT + v-i dp (см. разд. 2.4). Получаем, что наклон кривой фазового равновесия равен

(49)

dp As __ q

dT Av Tav

Второе начало: вычисление внутренней энергии. Второе начало термодинамики позволяет вывести важное соотношение для внутренней энергии простой системы, которое не может быть получено в рамках первого начала:

Покажем, как можно получить (18) из теоремы Карно. Рассмотрим (бесконечно) малый обратимый цикл Карно и изобразим его в координатах (р, V). Работа системы за цикл, равная площади маленького параллелограмма (рис. 18), не изменится при замене адиабат вертикальными отрезками, длина которых

- Умножив на высоту AV,

ATAV. Теплота, изотерме, равна

равна -^ A получим SA =

\О1 / V

на верхней

AV\

полученная

5Ql = AU + pdV T

р *„

где для приращения AU при постоянной температуре использовано (8). Из теоремы Карно и уравнения (17) имеем

_6А_ ЛТ \9TJv ЛТЛУ

AT

откуда получим (18).

Приведем несколько примеров применения формулы (18).

1) Внутренняя энергия идеального газа. Подставим в (18) уравне-

ние состояния р = —i/RT. В результате получим (-577) — 0> т.е.

V \oV /твнутренняя энергия идеального газа не зависит от объема.

2) Внутренняя энергия газа Ван-дер-Ваалъса. Выразив давление из уравнения состояния (3) и подставив в (18), приходим к формуле

dU\ ai/2 „

-Qy) - -ггг- Следовательно,

dV.

dU = Cv dT

роме того, имеем

. \ov Т dv\dT)v

т. е. Су не зависит от объема. В области температур, где Су слабо зависит от Т, можно записать

U = CyT-?£. (19)

3) Общая формула для Ср — Су- Подставляя (18) в уравнение (9) и фиксируя давление (р = const), получим:

Покажем, как можно получить (18) из теоремы Карно. Рассмотрим (бесконечно) малый обратимый цикл Карно и изобразим его в координатах (р, V). Работа системы за цикл, равная площади маленького параллелограмма (рис. 18), не изменится при замене адиабат вертикальными отрезками, длина которых

- Умножив на высоту AV,

ATAV. Теплота, изотерме, равна

равна -^ A получим SA =

\О1 / V

на верхней

AV\

полученная

5Ql = AU + pdV T

р *„

где для приращения AU при постоянной температуре использовано (8). Из теоремы Карно и уравнения (17) имеем

_6А_ ЛТ \9TJv ЛТЛУ

AT

откуда получим (18).

Приведем несколько примеров применения формулы (18).

1) Внутренняя энергия идеального газа. Подставим в (18) уравне-

ние состояния р = —i/RT. В результате получим (-577) — 0> т.е.

V \oV /т
внутренняя энергия идеального газа не зависит от объема.

2) Внутренняя энергия газа Ван-дер-Ваалъса. Выразив давление из уравнения состояния (3) и подставив в (18), приходим к формуле

dU\ ai/2 „

-Qy) - -ггг- Следовательно,

dV.

dU = Cv dT

Кроме того, имеем

. \ov Т dv\dT)v

т. е. Су не зависит от объема. В области температур, где Су слабо зависит от Т, можно записать

U = CyT-?£. (19)

3) Общая формула для Ср — Су- Подставляя (18) в уравнение (9) и фиксируя давление (р = const), получим:

(здесь использовано соотношение между производными, рассмотренное в конце разд. 2.1). Неотрицательность полученного выражения

следует из условия механической устойчивости: (~-г) ^ 0.

\ov /т

Литература

1. Детлаф А.А., Яворский Б.М. Курс физики.- М.: Высшая школа, 1999.

2. Зисман Г.А.., Тодес О.М. Курс общей физики: в 3 т.- Киев: Днипро, 1994.

3. Курс физики: Учебник для вузов в 2 т./ Под ред. В.Н. Лозовского,-СПб.: Лань, 2001

4. Лабораторные занятия по физике / Под ред. Л.Л. Гольдина,- М.: Физматлит, 1983/

5. Матвеев А.Н. Молекулярная физика.- М.: Высшая школа, 1987.

6. Савельев И.В. Курс общей физики: в 5 т. - М.: Наука..Физматлит, 1998 г.

7. Сивухин Д.В. Общий курс физики: в 5 т.- М.: Физматлит Изд.-во МФТИ 2002 г.

8. Трофимова Т.И. Курс физики. М.: Высшая школа, 2004