Кривые распределения

Кривая распределения — линия на плоскости, отражаю­щая зависимость между значениями рассматриваемой случай­ной величины и соответствующими им числами наблюдений.

Ноли на оси абсцисс откладывать значения варьирующего признака, а на оси ординат частоты, то, соединяя эти точки, получаем эмпири­ческую кривую распределения. Пользуются также кумулятивной кривой распределения, указывающей для каждого данного значения х частоту тех значений, которые не превосходят х. Кривая распреде­ления служит отправным пунктом статистического исследования варьирующего признака. Она является обобщенной характеристи­кой особенностей формы распределения. Кривая распределения вы­ражает закономерность распределения единиц совокупности по ве­личине варьирующего признака. Различают эмпирические и теоре­тические кривые распределения. Эмпирическая кривая — это фактическая кривая распределения, полученная по данным на­блюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение. Теоретическая кривая распределения — это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения. Кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой распределения вытянута — правая или левая — различают правостороннюю или левостороннюю асимметрию. Кривые распределения могут быть одно-, двух- и многовершинными.

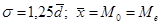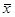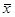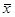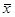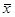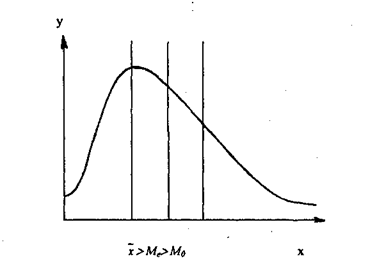
В нормальном ряду распределения размах вариации R = 6σ, . Если указанные соотношения нарушены, то это свидетельствует о наличии асимметрии распределения. Так, при М₀ < М_е < разности между - М₀ и - М _е положительные и асимметрия правосторонняя, а при М₀ > М_е > , наоборот, разности между - М₀ и 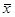- М_е отрицательные и симметрия левосторонняя (см. схемы 8.2, 8.3, 8.4, в которых показаны соотношения между средней, модой и медианой).

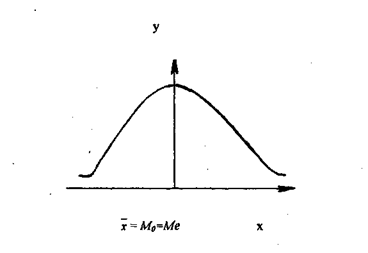Схема 8.4

Схема 8.2

В симметричном распределении центральный момент третьего порядка т₃ = 0, поэтому чем он больше, тем больше и асимметрия. Эта особенность и используется для характеристики асимметрий. Коэффициент, асимметрии равен отношению центрального момента третьего порядка к среднему квадратическому отклонению в кубе: 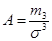. Если А>0, то асимметрия правосторонняя, а если А < 0, то асимметрия левосторонняя. Чем числитель ближе к 0, тем асим­метрия меньше.

Схема 8.5 Эксцессы распределения

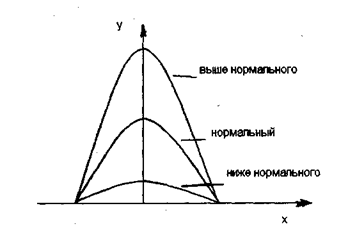Кривые распределения имеют различную островершинность. Крутизна, островершинность кривой распределения называется эксцессом. Различают эксцессы: нормальный, выше нормального и ниже нормального (схема 8.5).Для характеристики степени эксцесса применяют коэффици­ент эксцесса, который равен отношению центрального момента чет­вертого порядка к среднему квадратическому отклонению в четвер­той степени: 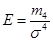. Если распределение нормальное, то эксцесс нормальный и равен 3. Поэтому если Е > 3, то эксцесс выше нор­мального, а если Е < 3, то эксцесс ниже нормального.