Критерий согласия

Для оценки близости эмпирического отношения к теоретическому нормальному пользуются специальными показателями, которые называются согласия. Они разработаны Пирсоном, Колмогоро­вым, Романовским и Ястремским. Наиболее простым и доступным является критерий Пирсона:

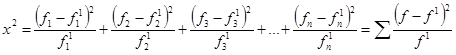
Чем меньше отклонение между эмпирическими и теоретиче­скими частотами, тем меньше значение х², а значит, теоретическое распределение лучше воспроизводит эмпирическое, и наоборот. Ес­ли эмпирические частоты совпадают с теоретическими, х² = 0.

Вычисление х² Пирсона связано с показателем, который назы­вается числом степеней свободы. Под числом степеней свободы К понимают количество независимых величин, которые могут прини­мать независимые значения, не изменяющие заданные характери­стики. Так, если средняя выработка рабочих участка равна 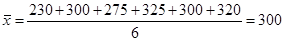деталей, то пять значений из шести могут быть произвольными, а шестое должно быть един­ственно возможным, при котором средняя выработка 300 деталей останется без изменений. В данном случае задан один параметр (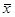), поэтому число степеней свободы будет равно: 6-1=5.

В нашем примере распределения ткачих по степени выполне­ния норм выделено семь групп, функция нормального распределе­ния имеет два параметра: 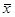и σ. Кроме того, исчисление критерия х² связано с ограничительным условием: ∑ f =∑ f¹.

Следовательно, число степеней свободы будет равно: К = 7 - 2 - 1=4. обозначим число групп т, число параметров r и получим К = т- r -1. По специальной таблице (приложение 2) находим зна­чение х², соответствующее данному числу степеней свободы и за­данной вероятности. По этой же таблице для заданного критерия х² при разных значениях степеней свободы можно определить вероят­ность того, что расхождение между теоретическими и эмпириче­скими частотами изучаемого ряда является случайным. Если факти­ческое значение критерия х² меньше табличного, то отклонение ме­жду эмпирическими и теоретическими частотами являются случай­ными, несущественными, и можно сделать вывод о том, что теоретическое распределение хорошо воспроизводит эмпирическое, и, наоборот, если фактическое значение больше табличного, то отклонения являются существенными и эмпирический ряд распределения не подчиняется закону нормального распределения.

Пример. Рассчитаем критерий х² по данным табл. 8.6.

Таблица 8.6

Распределение ткачих по степени выполнения норм, %

Номер группы	Эмпиричес­кие частоты (f)	Теоретичес­кие частоты (f1)	Отклонение (f – f1)	Квадрат отклонения (f – f1)2	Отношение
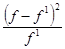
			-3		1,80
					0,32
					0,17
					0,57
					3,20
					0,12
					2,0
Итого			—	—	8,18

Следовательно, х² = 8,18. Теперь по таблице (приложение 2) находим критическое значение х² для заданной вероятности и числа степеней свободы. При К = 4 и Р = 0,95 получим х² = 9,49. В нашем примере фактическое значение х² = 8,18, а табличное х² = 9,49 т.е, фактическое значение меньше табличного. Следовательно, с вероятностью 0,95 можно утверждать, что распределение ткачих по степени выполнения норм подчиняется закону нормального распределения.

Критерий согласия Колмогорова (λ) рассматривает близость эмпирического и теоретического распределения путем сравнения их накопленных частот. Критерий лямбда равен максимальной разно­сти накопленных эмпирических и теоретических частот (без учета знаков), поделенный на корень квадратный из числа наблюдений.

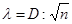
где D — максимальная разность накопленных эмпирических и теоретических частот, а п — объем совокупности. По сравнительной таблице (приложение 3) находим вероятность, с которой можно ут­верждать, что отклонение эмпирических частот от теоретических является несущественным, случайным, т.е. фактическое распреде­ление подчиняется закону нормального распределения.

Пример. Рассчитаем критерий λ по данным, приведенным в табл. 8.7.

Таблица 8.7

Распределение ткачих по степени выполнения норм, %

Номер группы	Эмпиричес­кие частоты (f)	Теоретичес­кие частоты (f1)	Накопленные частоты	Отклонение (Sf-Sf1=D) +,-
эмпирические (Sf)	теоретические (Sf1)
					+3 +1 -1 -5 +3 +2 -
Итого			—	—	—

В нашем примере D = 5, п = 100, откуда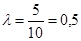. По таб­лице (приложение 3) определяем, что значению λ = 0,5 соответст­вует вероятность 0,963. Следовательно, с вероятностью 0,963 можно утверждать, что отклонение эмпирических частот от теоретических является случайным, т.е. распределение ткачих по степени выпол­нения норм выработки подчиняется закону нормального распреде­ления.

В явлениях различных аспектов рыночного хозяйства асим­метричные распределения встречаются значительно чаще, чем симметричные. Имеется много функций, характеризующих закономерности эмпирических асимметричных распределений. Некоторые асимметричные распределения могут быть приведены к форме, приближающейся к нормальной, путем преобразования значений признака х. Например, путем логарифмирования переменной х асимметричное распределение может быть приведено к нормальному. Распределение, которое с помощью логарифмирования пе­ременной х может быть приведено к нормальному, называется логарифмически нормальным распределением. Частоты такого распределения определяются на основе интегральной функции нор­мального распределения

Для объективной оценки близости эмпирических и теоретических частот также пользуются критериями согласия.

Вопросы для самоконтроля

1. Что такое динамический ряд и ряд распределения?

2. В чем сущность вариационного ряда распределения?

3. Что является одной из важных задач анализа рядов распределения?

4. Что выражают кривые распределения?

5. Какие кривые называются эмпирическими и теоретическими?

6. В чем сущность моделирования рядов распределения и его значение в анализе?

7. Как определяются коэффициенты асимметрии и что они характеризуют?

8. Как определяется коэффициент эксцесса и что он характеризует?

9. Какой функцией распределения характеризуется чисто нормальное распределение, ее формула и порядок вычисления теоретических частот?

10. Что характеризует критерий согласия?

11. Какова формула критерия согласия Персонса, с каким показателем связано его вычисление и применение в анализе?

12. Что представляет собой число степеней свободы и как оно определяется?

13. Какова формула критерия согласия Колмогорова и ее применение в анализе?

14. Что является логарифмически нормальным распределением и когда оно применяется?