2014-02-09
377
| № груп- пы | Группы ткачих по степени выполнения норм, % (х) | Число ткачих (f) | Нормированное
отклонение по
верхней границе
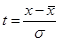
| Функ- ция распре- деления (F(ti)) | Вероят- ность (F(ti+i) - -F(ti)) | Теорети- ческие частоты (f) |
| А | Б | |||||
| До 100 | -1,67 | 0,047 | 0,047 | |||
| 100—110 | -0,94 | 0,174 | 0,12? | |||
| 110—120 | -0,22 | 0,413 | 0,230 | |||
| 120—130 | +0,51 | 0,095 | 0,282 | |||
| 130—140 | +1,23 | 0,891 | 0,196 | |||
| 140—150 | +1,96 | 0,975 | 0,084 | |||
| Свыше 150 | — | 1,000 | 0,025 | |||
| Итого | — | — | — | — |
Среднее выполнение норм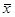 
= 123%, σ = 13,8.
Расчет производится следующим образом. По верхним границам интервалов определяется нормированное отклонение t. Так, для первой группы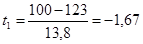 
, для второй — 
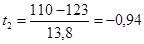и т.д. Затем по таблице (приложение 1) находим значение функции распределения F(t), потом вероятность F(ti+i) - F(ti) и теоретические частоты f. Значению t1 = -1,67 соответствует по таблице F(t) = 0,953. Но из симметричности нормального распределения следует, что F(-t) = 1 - F(t), т.е. F(-1,67) = 1 - 0,953 = 0,047. Для t2 = -0,94 F(t) = 0,826, откуда F(-0,94) = 0,174 и т.д. Вероятность того, что признак имеет значение в интервале от хi до хi+1, будет равна для первой группы 0,047, для второй — F(x2) - F(x1) = 0,174 - 0,047 = 0,127 и т.д. Теперь определяем теоретические частоты: 
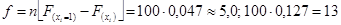и т. д.
|
|
|
Теоретическое распределение вероятностей и частот дает представление о форме, типе распределения, о закономерности, свойственной изучаемому явлению.
Эмпирические и теоретические распределения ткачих по степени выполнения норм приведены в схеме 8.6.
Схема 8.6
