Результаты тестирования по темам №1 и №2

Таблица 3.6

№ пп	1 2 3 4 5 6 7 8 9 10
ТЕМА №1 (баллы)	4,6 4,6 4,7 4,8 4,8 4,8 4,9 4,9 4,9 5,0
ТЕМА №2 (баллы)	12,4 12,7 13,0 13,3 13,1 13,2 13,5 13,5 13,6 13,7

Решение. Представим данные таблицы 3.6 в графической форме (рис. 3.14). Будем считать одну из величин зависимой, а другую - независимой. Результаты изучения ТЕМЫ № 2 (y_i) при фиксиро­ван­ных значениях результатов изучения ТЕМЫ № 1 (x_i) образовали на координатной плоскости гра­фик, анализ которого показывает, что в качестве первого приближения можно предположить, что в сред­нем результат изучения ТЕМЫ №2 линейно зависит от результатов изучения ТЕМЫ №1 (т.е. прини­маем модель простой линейной регрессии).

Найдем значения коэффициента регрессии (b) и свободного члена уравнения регрессии (a). По данным таблицы 3.6 находим значения промежуточных сумм (см. таблицу 3.7): 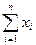= 48,0; 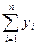=132,0; 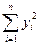=1743,94; 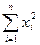= 230,56; 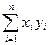= 634,08. Затем определяем значения средних арифметиче­ских:` x =4,8, ` y =13,2.

Тогда коэффициент регрессии b =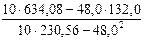» 3,0, свободный член уравнения рег­рессии a = 13,2 - 3,0·4,8 = - 1,2. Таким образом, уравнение регрессии имеет вид: y = -3,0 x – 1,2. Пря­мая, построенная по этому уравнению, показана на рис. 3.14.

Ответ: y = -3,0 x – 1,2.

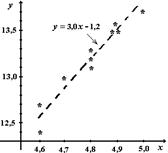
Эмпирическая линия регрессии изучения тем №1 и №2

Рис. 3.14

Полученное в примере 3.16 эмпирическое уравнение регрессии можно использо­вать для прогнозирования результатов изучения ТЕМЫ №2 по результатам изучения ТЕМЫ №1. Например, если в группе школьников, которая участвовала в экспери­менте, будет показан результат 5,2 балла при изучении ТЕМЫ №1, то можно ожи­дать, что результат изучения ТЕМЫ №2 будет: 3,0·5,2 – 1,2 = 14,4 (баллов). И это бу­дет наилучшим прогнозом, который можно сделать, используя модель линейной рег­рес­сии.

Корреляционный анализ состоит в определении степени связи между двумя слу­чайными величинами X и Y. В качестве меры связи используется коэффициент кор­реляции. Коэффициент корреляции оценивается по выборке объема n связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности X и Y.

Существует несколько типов коэффициентов корреляции, применение которых за­висит от предположений о совместном распределении величин X и Y. В предположе­нии о двумерном нормальном распределении генеральной совокупности, из которой получены экспериментальные данные пользуются коэффициентом корреляции Браве-Пирсона, который вычисляется по формуле:

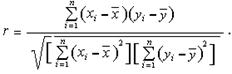Для практических расчетов удобна следующая формула коэффициента корреляции Браве-Пирсона:

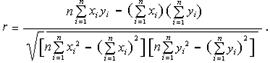(3.7)

Модель двумерного нормального распределения позволяет дать наглядную графи­ческую интерпретацию коэффициента корреляции.

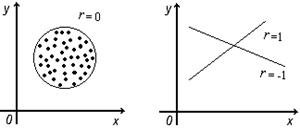
Если r = 0, то значения x_i, y_i полученные из двумерной нормальной совокупности, располагаются на графике в координатах x, y в пределах области, ограниченной ок­ружностью (рис. 3.15, а). В этом случае между случайными величинами X и Y отсутст­вует корреляция и они называются некоррелированными. Для двумерного нормаль­ного распределения некоррелированность означает одно­временно и независимость случайных величин X и Y.

Если r = 1 или r = -1, то между случайными величинами X и Y существует ли­ней­ная функциональная зависимость (Y = bX + a). В этом случае говорят о полной корре­ляции. При r = 1 значения x_i, y_i определяют точки, лежащие на прямой линии, имею­щей положительный наклон (с увеличением x_i значения y_i также увеличива­ются), при r = -1 прямая имеет отрицательный наклон (рис. 3.15, б).

Таким образом, коэффициент корреляции является мерой линейной связи между случайными величинами.

а) б)

в) г)

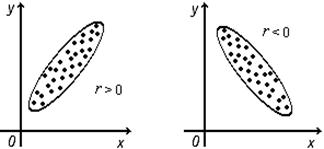
Геометрическая интерпретация коэффициента корреляции

Рис. 3.15

В промежуточных случаях (-1< r <1) точки, соответствующие значениям x_i, y_i, по­падают в область, ограниченную некоторым эллипсом (рис. 3.15, в, г), причем при r >0 имеет место положительная корреляция (с увеличением x_i значения y_i имеют тенден­цию к возрастанию), при r <0 корреляция отрицательная. Чем ближе r к ±1, тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии.

Пример 3.17. Вычислить коэффициент корреляции для распределений, заданных в таблице 3.6.

Решение. Вычислим значения промежуточных сумм, входящих в формулу (3.7): 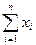=48,0; 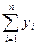=132,0; 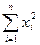=230,56; 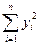=1743,94; 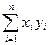=634,08. Промежуточные расчеты приведены в столбцах 2 - 6 таблицы 3.7.