Индексы Миллера

В кристалле

Образование плоскостей и направлений

Для обозначения кристаллографических плоскостей в настоящее время общепринятой является система индексов Миллера. Поясним ее сущность.

Выберем систему координат, оси которых совпадают с тремя ребрами элементарной кристаллической ячейки. Начало координат поместим в одном из узлов решетки, в котором пересекаются эти ребра. Осевые единицы выберем равными длине ребер кристаллической ячейки, т. е. масштаб по оси X будет равен а, по оси Y – b и по оси Z – с. Разномасштабность осей координат вполне оправдывает себя, так как позволяет ввести наиболее рациональную систему индексов. Положение любой плоскости в пространстве определяется тремя точками. В выбранной системе координат удобно в качестве трех опорных точек взять точки пересечения заданной плоскости с осями координат. Пусть определяемая узловая плоскость S пересекает оси координат в точках А, В, С (рисунок 2.5) и отсекает по осям отрезки х = 1, y = 2, z = 3.

Далее поступают по следующей схеме;

1) берут отрезки, отсекаемые плоскостью на осях координат: 1:2:3;

2) берут величины, обратные этим отрезкам: ;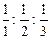

3) приводят к общему знаменателю: ;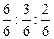

4) отбрасывают знаменатель: 6:3:2 – индексы Миллера для плоскости.

Миллеровские индексы плоскостей заключаются в круглые скобки – (632), знак отношения между индексами не ставится.

Если плоскость параллельна какой-либо оси, ее проекция на эту ось равна бесконечности. Для такой плоскости соответствующий индекс Миллера равен нулю. Если плоскость отсекает некоторый отрезок с отрицательным знаком, то соответствующий индекс Миллера будет также отрицательным, и черточка ставится сверху над индексами.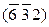

Рассмотрим пример кубической решетки. Нас интересует плоскость abcd (рисунок 2.6). Пусть ребро куба равно 1. Плоскость abcd имеет индексы Миллера (100). Если мы хотим обозначить не одну плоскость, а семейство плоскостей, то индексы Миллера берутся в фигурные скобки {100}.

Плоскость cdeq имеет индексы Миллера (101). Плоскость deg имеет индексы Миллера (111). Таким образом, мы описали три основные плоскости для кубической решетки (рисунок 2.7).

Индексы Миллера для направления представляют собой набор целых чисел, отношение которых друг к другу равно наименьшим проекциям вектора, параллельного выделенному направлению, но проходящего через начало координат. Индексы Миллера для направлений в отличие от индексов Миллера для плоскостей помещаются не в круглые, а в квадратные скобки.

Рассмотрим тот же пример кубической решетки (рисунок 2.6):

Направление ОХ: [100].

Направление ОА: [101].

Направление перпендикулярное плоскости (111): [111].

2.3.2

Плотность упаковки

Смоделируем частицы в узлах кристаллической решетки в виде идеальных (не деформированных) соприкасающихся шаров. Тогда плотность упаковки (коэффициент упаковки или компактность данной решетки) представляет собой отношение объема, занимаемого шарами в элементарной ячейке, ко всему объему самой элементарной ячейки. В качестве примера рассмотрим примитивную кубическую ячейку (рисунок 2.8).

Пусть радиус шара r. Тогда длина ребра куба 2r. Объем одного шара 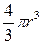. Внутрь попадает часть шара 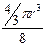. Таких шаров 8, и каждый принадлежит ячейке на 1/8. Тогда объем, занимаемый шарами внутри ячейки, 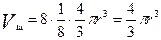. Объем ячейки: 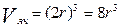. И плотность упаковки: f = 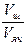= = 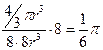0,52.