Теорема 1.1 (разложения).
Определитель матрицы 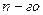 порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения
порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения
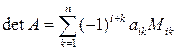 (1.4)
(1.4)
– разложение по 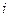 -й строке.
-й строке.
Пусть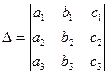 , тогда
, тогда 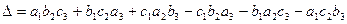 (1.5).
(1.5).
Докажем, что имеют место следующие равенства:
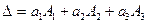 ,
, 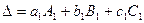 (1.6)
(1.6)
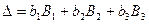
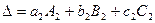 (1.7)
(1.7)
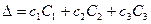
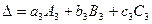 (1.8)
(1.8)
Чтобы доказать (1.6) достаточно записать правую часть формулы (1.5) в виде
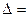
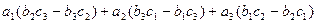 .
.
Величины, стоящие в скобках являются алгебраическими дополнениями матрицы 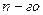 порядка элементов
порядка элементов 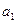 ,
, 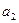 ,
, 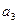 , т.е.
, т.е.
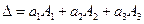 .
.
Равенства (1.7) и (1.8) доказываются аналогично.
 2014-02-09
2014-02-09 1074
1074








