2014-02-09
771
В трёхмерном случае уравнение приобретает вид:
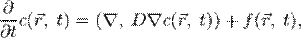
где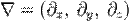 
— оператор набла, а 
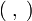— скалярное произведение. Оно также может быть записано как
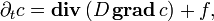
а при постоянном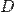 
приобретает вид:
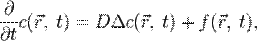
где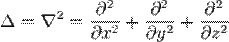 
— оператор Лапласа.
Обычно уравнение диффузии возникает из эмпирического (или как-то теоретически полученного) уравнения, утверждающего пропорциональность потока вещества (или тепловой энергии) разности концентраций (температур) областей, разделённых тонким слоем вещества заданной проницаемости, характеризуемой коэффициентом диффузии (или теплопроводности):
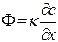(одномерный случай),
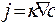(для любой размерности),
в сочетании с уравнением непрерывности, выражающим сохранение вещества (или энергии):
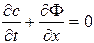(одномерный случай),
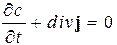(для любой размерности),
с учетом в случае уравнения теплопроводности ещё теплоёмкости (температура = плотность энергия / удельная теплоемкость).
