Модель межотраслевого баланса

ПРЕДИСЛОВИЕ

Моделирование экономических процессов впоследнее время является наиболее быстро развивающимся направлением экономической науки и ее важнейших приложений.

Главными задачами курса являются: 1) расширение и углубление теоретических знаний о количественных взаимосвязях и закономерностях экономического развития, механизмах управления народным хозяйством; 2) овладение методологией и методикой построения, анализа и применения математических моделей экономических процессов; 3) изучение наиболее характерных моделей и получение навыков практической работы с моделями, используемыми в практике.

В данном учебном пособии основное внимание уделяется приложениям математических методов к исследованию реальных экономических процессов. Показано, что математическое моделирование существенно расширяет возможности экономического анализа, повышает качество принимаемых экономических решений.

Изучение экономико – математических методов и моделей требует математической подготовки по линейной алгебре, дифференциальному исчислению, дифференциальным уравнениям, теории вероятностей и математической статистике. Математические докакзательства утверждений часто опускаются, поскольку основное внимание в учебном пособии уделяется приложениям математического аппарата.

8.1. Схема модели межотраслевого баланса в системе национальных счетов. Межотраслевой баланс (МОБ) представляет собой экономико-математическую модель процесса воспроизводства, которая в развернутом виде отражает взаимосвязи по производству, распределению, потреблению и накоплению общественного продукта в разрезе отраслей народного хозяйства и в единстве материально-вещественного и стоимостного аспектов воспроизводства.

Межотраслевые балансы могут разрабатываться на плановый и отчетный период в натуральном, натурально-стоимостном и стоимостном выражении.

Межотраслевые балансы в натуральном выражении (в физических измерителях) охватывают только важнейшие виды продукции. Натурально-стоимостной (баланс смешанного типа) охватывает весь общественный продукт. Стоимостной баланс характеризует процесс воспроизводства в денежном выражении.

При построении межотраслевого баланса используется понятие "чистой" отрасли, т.е. условной отрасли, объединяющей все производство данного продукта независимо от ведомственной подчиненности и форм собственности предприятий и фирм. Переход от хозяйственных отраслей к чистым, требует специального преобразования реальных данных хозяйственных объектов, например агрегирования (объединения) отраслей, исключения внутриотраслевого оборота.

Межотраслевой баланс может быть представлен в виде схемы и модели. Схема межотраслевого баланса производства и распределения общественного продукта в стоимостном выражении приведена в таблице 8.1 и состоит из трех квадрантов. Все народное хозяйство в схеме разбито на 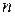отраслей, в которые включаются как отрасли материального производства, так и сфера услуг. Вся продукция отраслей разделена на промежуточную и конечную. Первый квадрант отражает структуру промежуточного потребления и промежуточных затрат. Второй квадрант – отраслевую и материально-вещественную структуру конечного использования общественного продукта. Третий квадрант – стоимостную структуру валового внутреннего продукта.

На схеме использованы обозначения:

· в первом квадранте переменные 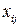выражают поставку продукции отрасли i (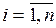) на производство продукции отрасли j ();

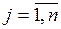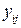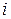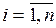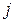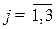· во втором квадранте переменные отражают поставку продукции из -той () отрасли для формирования -го () элемента конечного использования;

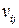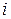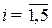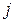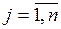· в третьем квадранте переменные характеризуют объем -го () элемента добавленной стоимости в -ой () отрасли;

· переменные 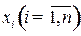характеризуют объем валовой продукции 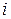-той отрасли.

Набор отраслей первого квадранта предопределяет формирование столбцов второго и строк третьего квадрантов.

В столбце второго квадранта «Конечное потребление» отражаются:

- потребление конечных товаров и материальных услуг, купленных домашними хозяйствами за счет своих доходов, продукция подсобного личного хозяйства и другие натуральные доходы домашних хозяйств, а также покупка государственными учреждениями и некоммерческими организациями товаров и услуг для передачи домашним хозяйствам;

- объем платных услуг, потребляемых домашними хозяйствами за счет своих доходов, а также стоимость нерыночных услуг, оказываемых бюджетными организациями в сфере здравоохранения, образования, социального обеспечения, культуры, искусства.

В столбце «Валовое потребление» отражены валовые накопления основного капитала и изменение запасов материальных оборотных средств в разрезе отраслей материального производства.

В столбце «Экспорт-импорт» отражается экспорт–импорт товаров и нефакторных услуг.

Экономическое содержание элементов столбцов II квадранта определяется счетами использования доходов, капитальных затрат, текущих операций по внешнеэкономическим связям.

Показатели III квадранта аналогичны показателям национальных счетов, и в первую очередь, счетов образования и первичного распределения доходов.

При указанных принципах формирования показателей межотраслевого баланса СНС, величины 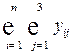и 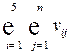представляют собой валовой внутренний продукт; величины характеризуют производственное потребление продукции 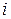-ой отрасли; величины 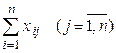- суммы производственных затрат 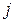-ой отрасли. Величина 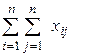равна сумме производственных затрат всех отраслей и характеризует промежуточный продукт народного хозяйства.

В схеме МОБ совмещаются два частных межотраслевых баланса - баланс распределения продукции (I и II раздел) и баланс затрат (I и III раздел).

Производящие отрасли	Потребляющие отрасли	Промежуточ- ное потребление	Конечное использование	Валовой выпуск
		…	n	Конечное потребление	Валовое накопление	Сальдо экспорта-импорта	Итого
….	…	…	… … … …	…	…	…	…	…	…	…
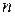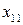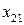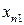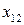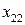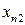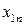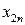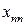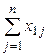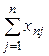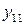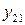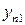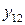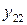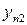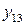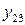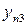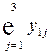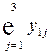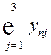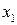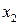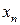Промежуточные затраты			…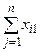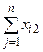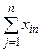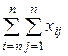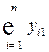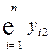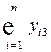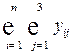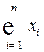
Потребление основного капитала			…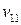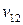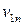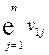
Заработная плата			…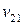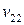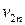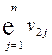
Прибыль			…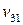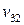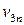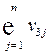
Косвенные налоги			…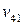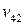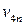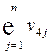
Субсидии			…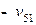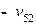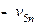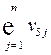
Валовая добавленная стоимость			…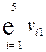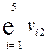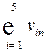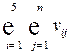
Валовой выпуск			…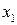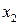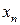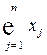

Таблица 8.1. Схема отчетного МОБ в денежном выражении СНС

8.2. Математическая модель отчетного межотраслевого баланса. Математическая модель отчетного МОБ выражается в виде двух систем линейных уравнений. Поскольку в I и II квадрантах представлено распределение произведенной продукции на нужды текущего промежуточного потребления и конечного использования, то соотношение показателей выражается системой уравнений

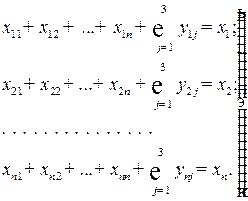(8.1)

В I и III квадрантах в отраслевом разрезе представлены затраты, осуществляемые на производство продукции и валовую добавленную стоимость. Соотношение показателей описывается следующей системой:

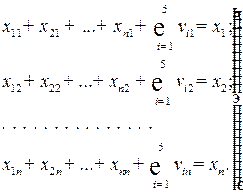(8.2)

Просуммировав все уравнения системы (8.1), получим равенство:

.

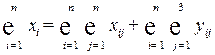Аналогично, суммирование уравнений системы (8.2) определяет равенство:

.

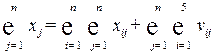Поскольку 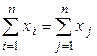, тo .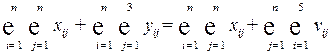

Откуда следует, что

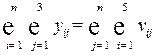
объемы конечного продукта по материально-вещественному и стоимостному составу равны.

Модель МОБ строится исходя из предположения, что нормативы затрат не зависят от объема выпуска продукции. Нормативы, называемые на макроуровне коэффициентами прямых затрат, или технологическими коэффициентами, выражаются соотношениями , .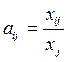

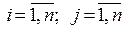При этом предположении величины межотраслевых поставок могут быть определены по формулам

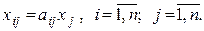(8.3)

Коэффициенты прямых затрат 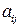, 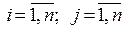показывают, какое количество продукции 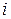-ой отрасли необходимо для производства единицы валовой продукции 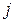-ой отрасли. Матрица

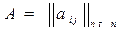
называется матрицей коэффициентов прямых затрат.

Подставив в систему (8.1) соотношения (8.3), получим систему

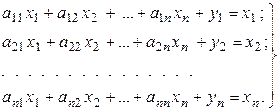(8.4)

Обозначим через 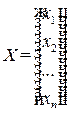матрицу-столбец валового выпуска продукции, 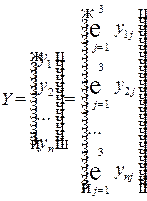матрицу-столбец конечной продукции, тогда воспользовавшись умножением матриц систему (8.4) можно записать в виде матричного уравнения:

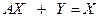, (8.5)

которое называется уравнением Леонтьева. Уравнение (8.5) можно переписать в виде 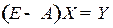, (8.6)

где 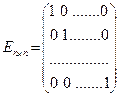- единичная матрица. Умножив уравнение (8.6) слева на обратную матрицу 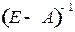, найдем матрицу валового выпуска продукции 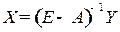. (8.7)

Матрицу 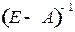называют матрицей коэффициентов полных затрат и обозначают

.

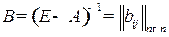Матрица В называется также обратной матрицей Леонтьева или мультипликатором Леонтьева.

8.3. Экономическая сущность и свойства коэффициентов прямых и полных затрат. Требованияобщественного производственногопроцесса накладывают ограничения на элементы матриц 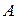и 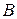. Отметим наиболее важные из них.

1) Матрица коэффициентов прямых затрат 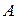является неотрицательной матрицей. Это означает, что коэффициенты 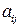неотрицательные величины, т.е.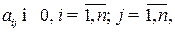так как неотрицательны величины 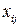и положительны валовые выпуски отраслей : .

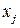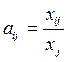2) Все диагональные элементы 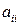матрицы 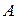должны быть меньше 1, ибо в противном случае производство лишается всякого смысла, .

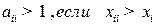3) Произведения элементов симметричных относительно главной диагонали должны быть меньше единицы, т.е. .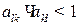

4) Норма матрицы 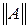меньше единицы, т. е. 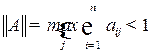. Если же для некоторой 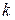-ой отрасли 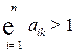, то экономически это значит, что отрасль настолько убыточна, что ее расходы на амортизацию и оплату труда перекрывают доходы. Из того, что норма матрицы 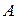меньше единицы следует, что 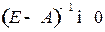; все собственные значения 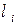матрицы 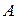по модулю меньше единицы, а наибольшее собственное значение положительно; все главные миноры матрицы 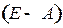положительны и меньше единицы.

Из существования обратной матрицы 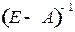следует, что матрица 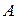продуктивна. Следовательно, продуктивность матрицы 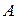в МОБ может определяться неравенствами 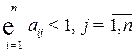. Матрица 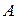называется продуктивной, если существует матрица 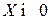, позволяющая получить матрицу конечной продукции .

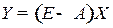5) Матрица коэффициентов полных затрат 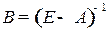является неотрицательной матрицей, так как коэффициенты полных затрат 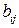показывают, какой должен быть валовой выпуск 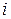-той отрасли для того, чтобы обеспечить выпуск единицы конечной продукции 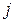-той отрасли.

6) Коэффициенты полных затрат 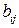не меньше коэффициентов прямых затрат, т.е. .

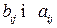7) Все диагональные элементы 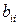матрицы 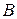должны быть не меньше единицы, т.е. 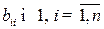, так как они характеризуют совокупность прямых и косвенных затрат.

Используя матрицу полных затрат 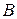можно: 1) провести анализ взаимосвязей для выпуска конечной и валовой продукции; 2) определить полные затраты народного хозяйства для выпуска конечной продукции; 3) оценить влияние на экономику изменений в структуре составляющих конечной продукции; 4) рассчитать какое влияние окажет на народное хозяйство изменение коэффициентов прямых затрат; 5) определить структуру основных фондов производственных отраслей, необходимую для выпуска данного объема конечной продукции.

Сформулированный экономический смысл коэффициентов полных затрат будет понятен, если записать матричное уравнение (8.7) в виде системы:

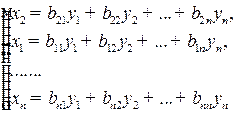(8.8)

Предположим, что осуществляется выпуск конечной продукции лишь одной (для определенности) первой отрасли:. Из уравнений (8.8) следует, что для того, чтобы обеспечить выпуск конечной продукции в указанном объеме , необходимо обеспечить валовой выпуск продукции 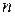отраслей в объемах: 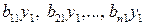. Эти значения получим, если подставить в систему (8.8) значения 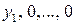. Следовательно, элементы первого столбца матрицы 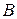показывают какое количество валовой продукции 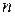отраслей необходимо для производства единицы конечной продукции первой отрасли. Аналогично можно показать, что элементы 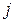-го столбца матицы 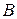определяют количество валовой продукции 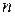отраслей, необходимых для производства единицы конечной продукции 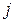-ой отрасли.

8.4. Использование модели МОБ в исследовании взаимосвязи отраслевых структур валового выпуска и конечного спроса. Матричное уравнение 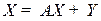, связывающее валовой выпуск отраслей (матрица 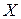) и конечную продукцию (матрица 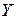), является основным в межотраслевых моделях. Такая взаимосвязь позволяет решать как прямую задачу: определение объема и отраслевой структуры валового выпуска в зависимости от объема и отраслевой структуры конечной продукции; так и обратную: определение объема и отраслевой структуры конечного использования в зависимости от объема и отраслевой структуры валового выпуска.

При решении первой задачи предполагается, чтообъемы и отраслевая структура конечной продукции задана и что в прогнозном периоде не произойдет существенных технологических изменений по сравнению с отчетным периодом, т.е. технологическая матрица 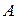постоянная. Тогда из матричного уравнения 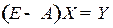находим объем и отраслевую структуру валового выпуска продукции:

.

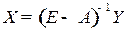Из этого уравнения можно определить, в какой степени изменение платежеспособного конечного спроса повлияет на объемы производства валовой продукции отраслей.

Если же будут заданы объемы и отраслевая структура валового выпуска, матрица 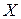, то, воспользовавшись уравнением

,

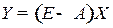можно найти объемы и отраслевую структуру конечной продукции. Следовательно, можно найти, в какой степени спад производства в отдельных отраслях отразится в целом на величине конечного использования продукции отраслей и на валовом накоплении.

Оценку интенсивности влияния конечного спроса и технологических изменений на структурные сдвиги в экономике, т. е. на изменения в структуре валового выпуска, определяем из матричного уравнения: 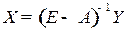. Структурные сдвиги в экономике за период 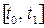определим по формуле 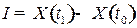, используя следующую цепочку соотношений:

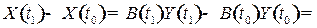
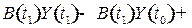
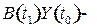
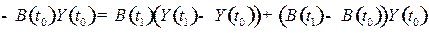, (8.9)

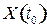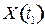где и матрицы валовых выпусков отрасле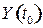й;

и 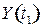матрицы конечного спроса;

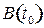и 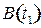матрицы коэффициентов полных затрат,

соответственно в периоды 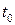и .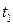

Первое слагаемое формулы (8.9) определяет величину структурных сдвигов, обусловленных изменением конечного спроса; второе слагаемое определяет структурные сдвиги под влиянием технологических изменений. Для выявления реальных структурных изменений следует исключить из анализа воздействие ценового фактора.

Пример 8.1. Пустьматрица коэффициентов прямых затрат в модели Леонтьева равна: 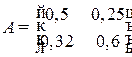, а матрица-столбец конечного использования 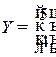. Найти матрицу-столбец валового выпуска продукции и сформулировать экономическую интерпретацию коэффициентов прямых и полных затрат.

Решение. Для определения объема и структуры валового выпуска продукции воспользуемся формулой: 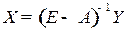, в которой неизвестной является матрица . Определим вначале матрицу 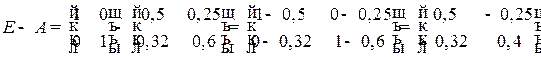и, применяя метод Гаусса, найдем обратную матрицу:

.

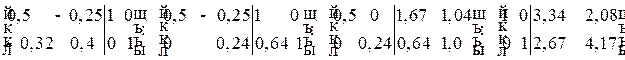Следовательно, .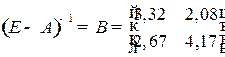

Тогда объем и структура валового выпуска продукции определяется матрицей: .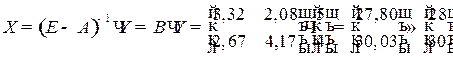

Проанализируем значения коэффициентов матриц 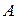и 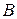с экономической точки зрения. Предположим, что данные отчетного МОБ измеряются в млрд. руб. Тогда:

- коэффициент 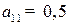матрицы 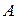означает, что для производства валовой продукции первой отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции первой отрасли на сумму 0,5 млрд. руб.;

- коэффициент 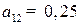матрицы 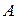означает, что для производства валовой продукции второй отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции первой отрасли на сумму 0,25 млрд. руб.;

- коэффициент 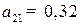матрицы 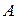означает, что для производства валовой продукции первой отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции второй отрасли на сумму 0,32 млрд. руб.; и т. д.

- коэффициент 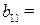3,32 матрицы 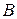означает, что для производства конечной продукции первой отрасли на сумму 1 млрд. руб., необходимо израсходовать валовой продукции первой отрасли на сумму 3,32 млрд. руб., так как коэффициенты полных затрат характеризуют совокупность прямых и косвенных затрат;

- коэффициент 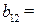2,08 матрицы 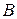означает, что для производства конечной продукции второй отрасли на сумму 1 млрд. руб., необходимо израсходовать валовой продукции первой отрасли на сумму 2,28 млрд. руб., и т. д.

Из экономической интерпретации коэффициентов 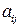и 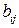вытекают их некоторые свойства.

Показатель 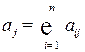определяет материалоемкость 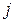- той отрасли, а средневзвешенная материалоемкость отраслей 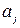, весами которых является валовая продукция отраслей 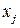, равна материалоемкости общественного продукта:

.

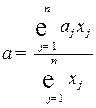Показатель 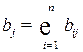определяет потребность в валовой продукции для получения единицы конечной продукции 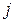- той отрасли, а средневзвешенная потребность в валовой продукции 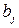, весами которой является объем конечной продукции, равна количеству валовой продукции, необходимой для производства единицы ВВП:

.

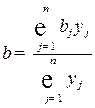Показатель 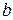характеризует соотношение ВВП и валовой общественной продукции.

Пример 8.2. Пусть задана матрица прямых затрат 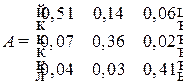. Определить конечное использование продукции каждой отрасли при условии, что валовой выпуск отраслей в прогнозном периоде в сопоставимых ценах (млрд. руб.) определяется матрицей .

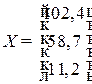Решение. Для определения объема и структуры конечного использования продукции воспользуемся уравнением 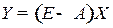, в котором неизвестной является матрица 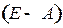. Вычислив матрицу

=

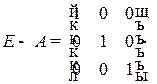
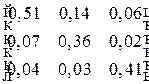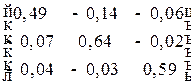
и воспользовавшись правилом умножения матриц, найдем конечное использование продукции отраслей в сопоставимых ценах (млрд. руб.):

==.

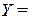
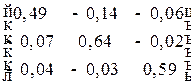
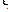
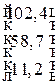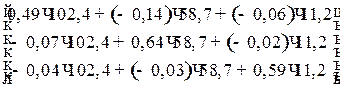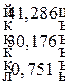Спрогнозировав конечное потребление (например, КП= 50 млрд. руб.) и сальдо экспорта-импорта (СЭИ= - 9 млрд. руб.) можно оценить валовое накопление (ВН) в рамках заданного валового выпуска: ВН= 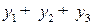- КП – СЭИ= =41,286+30,176+0,751 - 50 + 9= 31,212(млрд. руб.).

8.5. Использование статической модели МОБ в прогнозировании цен. Прогнозирование цен осуществляется на основе первого и третьего квадрантов МОБ с использованием системы уравнений

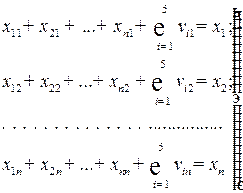, (8.2)

которая преобразуется, после подстановки 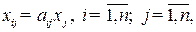и деления на 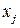, в систему:

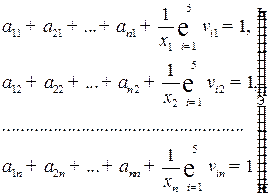. (8.10)

Прогнозирование на период 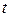осуществляется на основе данных МОБ предшествующего периода 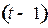. Структура затрат в сопоставимых ценах на рассматриваемом отрезке времени 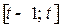предполагается неизменной. Пусть изменение цен в 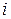-той отрасли характеризуется индексом цен 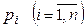, однако структура затрат в сопоставимых ценах осталась неизменной. При этих предположениях, элементы I и III квадрантов схемы МОБ запишутся как показано в таблице 8.2, поскольку элементы валовой добавленной стоимости являются составляющими цены.

Как следует из систем (8.2) и (8.10), балансовые соотношения для прогнозирования цен примут вид:

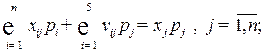(8.11)

(8.12)

Системы (8.11) и (8.12) являются базовыми балансовыми моделями прогнозирования цен в отраслях экономики.

Таблица 8.2

Схема первого и третьего квадрантов МОБ в текущих ценах

Производящие отрасли	Потребляющие отрасли
		…	n
			…
			…
…	…	…	…
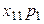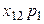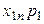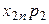n			…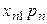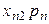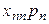
Потребление основного капитала			…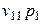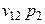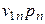
Заработная плата			…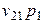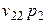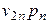
Прибыль			…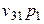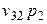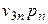
Косвенные налоги			…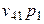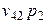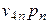
Субсидии	-	-	…	-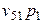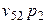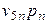
Валовой выпуск			…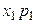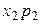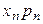

Пример 8.3. Пусть задана структура затрат последнего отчетного периода, представленная в таблице 8.3. Учитывая, что реальная динамика затрат в прогнозном периоде остается неизменной, оценить какое влияние оказывает увеличение цены на продукцию третьей отрасли в 5 раз на изменение цен в других отраслях.

Решение. Поскольку структура затрат в прогнозном периоде остается неизменной, то увеличение цены на продукцию третьей отрасли в 5 раз приведет к увеличению цен на продукцию первой и второй отрасли в 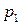и 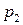раз соответственно.

Таблица 8.3.

Схема первого и третьего квадрантов трехотаслевого МОБ в текущих ценах

Производящие отрасли	Потребляющие отрасли
	67,5	120,3	84,7
	59,4	102,1	92,2
	48,5	100,2	72,1
Потребление основного капитала	210,1	200,2	97,3
Заработная плата	340,6	326,5	298,5
Прибыль	91,1	49,4	56,3
Косвенные налоги	46,2	50,1	41,1
Субсидии	-300	-250	-270
Валовой выпуск

Из условия задачи следует, что задан индекс цен на продукцию третьей отрасли. Следовательно, величина затрат на продукцию третьей отрасли не влияет на формирование цены в этой отрасли. Для определения изменения цен в первой и второй отрасли составим систему вида (8.11). Она будет состоять из двух балансовых уравнений для первой и второй отрасли:

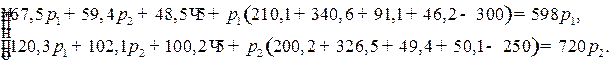
После приведения подобных, получим систему:

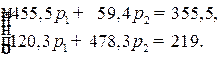
Для ее решения воспользуемся методом Гаусса. Составим расширенную матрицу системы и, применяя элементарные преобразования, приведем ее к виду, где слева от вертикальной черты будет записана единичная матрица:

.

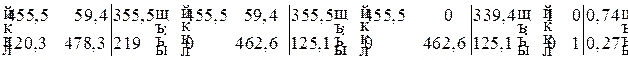Тогда 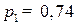и 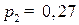. Таким образом, повышение цены на продукцию третьей отрасли в 5 раз приведет к повышению цены на продукцию третьей отрасли в 0,74 раза, и второй отрасли – в 0,27 раза, при условии, что индекс роста цен всех элементов добавленной стоимости совпадает с индексом роста цен.