Уравнение конвективной диффузии математически описывает процесс массопереноса в одной фазе и для вывода критериев подобия оно должно быть дополнено соответствующими условиями, характеризующими массообмен на границе раздела фаз.
При одномерном диффузионном потоке в соответствии с 1-м законом Фика к поверхности раздела фаз будет передано количество вещества:
dM = - D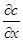 dFdτ. По Закону Щукарева: dM =
dFdτ. По Закону Щукарева: dM = 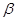 dF Δ C dt, отсюда:
dF Δ C dt, отсюда:
 - D
- D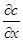 =
=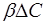 .
.
На основе теории подобия после деления правой части на левую без учета знаков математических операций, замены x на 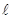 (определяющий размер) получим:
(определяющий размер) получим:
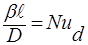 - диффузионный критерий Нуссельта – характеризует массообмен на границе фаз и является аналогом теплового критерия Нуссельта.
- диффузионный критерий Нуссельта – характеризует массообмен на границе фаз и является аналогом теплового критерия Нуссельта.
Из дифференциального уравнения конвективной диффузии для одномерного случая:
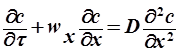
 путем деления правой части уравнения на 1-ое слагаемое левой части, после преобразований получаем:
путем деления правой части уравнения на 1-ое слагаемое левой части, после преобразований получаем:
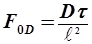 - диффузионный критерий Фурье, который характеризует нестационарный диффузионный процесс.
- диффузионный критерий Фурье, который характеризует нестационарный диффузионный процесс.
Поделив 2-ое слагаемое левой части на правую, получим:
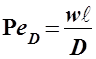 - диффузионный критерий Пекле, который характеризует подобие полей концентраций по длине пути.
- диффузионный критерий Пекле, который характеризует подобие полей концентраций по длине пути.
Гидродинамическое подобие в массообменных аппаратах характеризуется критерием: Re=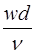 ;
; 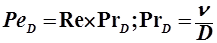 ,
,
PrD - диффузионный критерий Прандтля, характеризует подобие полей физических величин.
Учитывая, что критерий NuD является определяемым, общее критериальное уравнение конвективной диффузии записывается следующим образом: 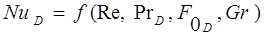 .
.
При вынужденном движении исключается Gr, т.к. естественной конвекцией можно пренебречь, и 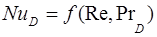 или
или 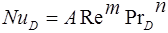 .
.
Для естественной конвекции из общего уравнения выпадает критерий Re: 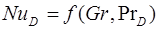 или
или 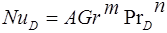 .
.
Значения коэффициентов А, m и n определяются исходя из опытных данных для конкретных случаев диффузионных процессов.
Критерий NuD вычисляется по полученным критериальным уравнениям и по нему определяют 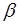 :
: 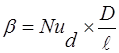 .
.
 2014-02-09
2014-02-09 5449
5449








