Подвергая обследованию каждую единицу данного рода, мы получаем генеральную совокупность. В ряде случаев: когда не определены границы генеральной совокупности, когда ограничены ресурсы, когда в результате наблюдения единица наблюдения уничтожается используется выборочный метод.
Выборочная совокупность – часть генеральной совокупности, отобранная т.о. когда каждая единица имеет равную возможность попасть в выборку.
Выборочная совокупность – модель генеральной совокупности,. По характеристикам выборочной совокупности, мы оцениваем генеральную совокупность.
Характеристиками являются:
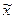 Средняя выборочная
Средняя выборочная
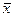 Генеральная средняя
Генеральная средняя
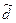 Доля выборочной совокупности, по которой мы оцениваем долю генеральной совокупности
Доля выборочной совокупности, по которой мы оцениваем долю генеральной совокупности
Любая модель отличается от оригинала, т.е. характеристики выборочной совокупности будут иметь некоторые отличия от характеристик генеральной совокупности. Эти отличия называются ошибками выборки.
Ошибки выборки бывают 2х родов:
1) ошибка неправильно организованной выборки (систематическая ошибка репрезентативности)
2) случайная ошибка репрезентативности
Т. к. мы выполняем условия равные возможности попасть в выборку для каждой единицы, то для оценки величины средней случайной ошибки m, используем методы мат. статистики. Исчисление величины m зависит от способа формирования выборочной совокупности.
Виды выборок:
- Собственно-случайный отбор осуществляется без расчленения совокупности на группы, и методом случайного извлечения единиц (лотерея, таблица, сл числа) Собственно-случ отбор м.б. повторным (схема возвращенного шара)
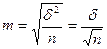
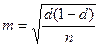
Собственно-случайная бесповторная выборка (схема невозвращенного шара)
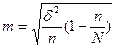
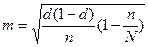
- Механистический отбор. Совокупность делится на столько групп, сколько требуется единиц для выборки.
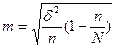
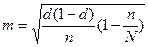
- Типичный (типологический стратифицированный районированный). Отбор из единиц производится из типических групп пропорционально их численности в группе
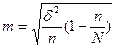
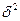 - средняя из внутригрупповых дисперсий
- средняя из внутригрупповых дисперсий
В каждой выделенной группе мы находим дисперсию, а потом среднюю дисперсю из всех.
- Серийный (гнездовой, кластерный) отбор. Это отбор из некоторых серий. Этот отбор чаще всего используется, когда ограничены средства и единицы подвергаются уничножению. В каждой серии единицы подвергаются сплошному отбору
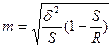 - ошибка средней для серийного отбора
- ошибка средней для серийного отбора
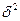 - межсерийная дисперсия
- межсерийная дисперсия
S - число серий
- Многоступенчатая выборка. Несколько стадий отбора: на каждой стадии своя единица отбора
- Многофазная выборка. Несколько ступеней наблюдения. Одна и та же единица наблюдения, но разный перечень признаков
- Комбинированный отбор
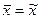 с ошибкой
с ошибкой 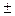 m – точечная оценка генеральной средней
m – точечная оценка генеральной средней
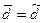 с ошибкой
с ошибкой 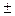 m
m
Важно так же определить интервал в пределах которого с заданной нами вероятностью окажется генеральная средняя.
Исчисляется предельная ошибка выборки 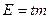
t- кратность ошибки m, коэффициент доверия, t-стьюдента. Его величина зависит от объема совокупности V=n-1 и доверительной вероятность Р
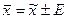
 2014-02-09
2014-02-09 377
377








