Наибольший термический КПД в заданном диапазоне температур имеет цикл Карно. При его осуществлении предполагается использование горячего источника с постоянной температурой, т. е. фактически с бесконечной теплоемкостью. Между тем на практике в работу превращается теплота продуктов сгорания топлива, теплоемкость которых конечна. Отдавая теплоту, они охлаждаются, поэтому осуществить изотермическое расширение рабочего тела при максимальной температуре горения не удается. В этих условиях необходимо установить общие принципы, определяющие наибольшую термодинамическую эффективность теплосилового цикла, в частности, с позиций потери эксергии.
Эксергетический и термический коэффициенты полезного действия позволяют оценивать термодинамическое совершенство протекающих в тепловом аппарате процессов с разных сторон. Термический КПД, а также связанный с ним метод тепловых балансов позволяют проследить за потоками теплоты, в частности рассчитать, какое количество теплоты превращается в том или ином аппарате в работу, а какое выбрасывается с неиспользованным (например, отдается холодному источнику). Потенциал этой сбрасываемой теплоты, ее способность еще совершить какую-либо полезную работу метод тепловых балансов не рассматривает.
Эксергетический метод, наоборот, позволяет проанализировать качественную сторону процесса превращения теплоты в работу, выявить причины и рассчитать потери работоспособности потока рабочего тела и теплоты, а значит, и предложить методы их ликвидации, что позволит увеличить эксергетический КПД и эффективность работы установки. Поэтому в дальнейшем анализе эффективности работы тепловых установок мы будем параллельно пользоваться как эксергетический методом, так и методом балансов теплоты.
Назначением теплосиловых установок является производство полезной работы за счет теплоты. Источником теплоты служит топливо, характеризующееся определенной теплотой сгорания Q. Максимальная полезная работа 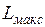 , которую можно получить, осуществляя любую химическую реакцию (в том числе и реакцию горения топлива), определяется соотношением Гиббса (1839—1903) и Гельмгольца (1821 —1894), получаемым в химической термодинамике:
, которую можно получить, осуществляя любую химическую реакцию (в том числе и реакцию горения топлива), определяется соотношением Гиббса (1839—1903) и Гельмгольца (1821 —1894), получаемым в химической термодинамике:
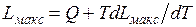
Эта работа может быть меньше теплоты сгорания Q, а может быть и больше, в зависимости от знака 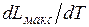 . Расчеты показывают, что для большинства ископаемых топлив
. Расчеты показывают, что для большинства ископаемых топлив 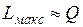 . Таким образом, эксергия органического топлива (в расчете на единицу его массы) примерно равна теплоте его сгорания, т. е. теоретически в работу можно превратить весь тепловой эффект реакции, например, в топливных элементах. Физически это понятно, поскольку в своей основе химическая реакция связана с переходом электронов в веществе; организовав этот переход, можно сразу получить электрический ток.
. Таким образом, эксергия органического топлива (в расчете на единицу его массы) примерно равна теплоте его сгорания, т. е. теоретически в работу можно превратить весь тепловой эффект реакции, например, в топливных элементах. Физически это понятно, поскольку в своей основе химическая реакция связана с переходом электронов в веществе; организовав этот переход, можно сразу получить электрический ток.
В теплосиловых установках энергия топлива сначала превращается в тепловую путем его сжигания, а полученная теплота используется для выработки механической энергии. Поскольку горение — неравновесный процесс, он связан с потерей работоспособности тем большей, чем ниже температура 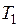 получаемых продуктов сгорания. В современных паровых котлах, например, где теоретическая температура горения достигает 2000°С и более, потери эксергии при горении составляют 20—30%.
получаемых продуктов сгорания. В современных паровых котлах, например, где теоретическая температура горения достигает 2000°С и более, потери эксергии при горении составляют 20—30%.
Выше уже отмечалось, что основными причинами, снижающими эффективность тепловых процессов, являются трение и теплообмен при конечной разности температур. Вредное влияние трения не нуждается в пояснениях. Рассмотрим передачу теплоты от продуктов сгорания топлива к воде и пару в паровом котле.
Продукты сгорания, охлаждаясь в изобарном процессе 1-2 (рис. 6.1), отдают теплоту  , которая затрачивается на нагрев воды (линия 3-4), ее испарение (линия 4-5) и перегрев пара до нужной температуры (линия 5-6). Если не учитывать теплопотери в окружающую среду, то количество теплоты, отданной газами, будет равно количеству теплоты
, которая затрачивается на нагрев воды (линия 3-4), ее испарение (линия 4-5) и перегрев пара до нужной температуры (линия 5-6). Если не учитывать теплопотери в окружающую среду, то количество теплоты, отданной газами, будет равно количеству теплоты 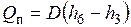 , воспринятой водой и паром:
, воспринятой водой и паром: 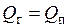 или
или 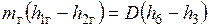 .
.
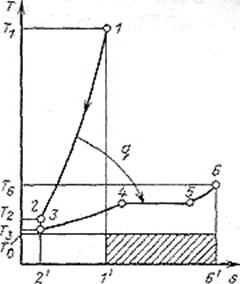
Рисунок 8.1 - К расчету по Т,s -диаграмме эксергетических потерь
при неравновесном теплообмене
Здесь 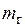 и D — массовые расходы газов и пара, а
и D — массовые расходы газов и пара, а 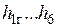 — удельные энтальпии соответствующих веществ в соответствующих состояниях.
— удельные энтальпии соответствующих веществ в соответствующих состояниях.
Чтобы изобразить описанные процессы в T,s -диаграмме водяного пара в одном масштабе, отложенные на ней значения энтропии воды и пара отнесены к 1 кг, а энтропии греющих газов — к их количеству, приходящемуся на 1 кг пара, т. е. 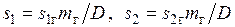 где
где  — удельная энтропия газа. Для удобства сравнения принято также общее начало отсчета энтропии, т.е.
— удельная энтропия газа. Для удобства сравнения принято также общее начало отсчета энтропии, т.е. 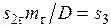 . В таком случае площадь 1-1'-2'-2, представляющая собой количество отданной газом теплоты, и площадь 2'-3-4-5-6-6', эквивалентная количеству теплоты, воспринятой паром, равны друг другу.
. В таком случае площадь 1-1'-2'-2, представляющая собой количество отданной газом теплоты, и площадь 2'-3-4-5-6-6', эквивалентная количеству теплоты, воспринятой паром, равны друг другу.
Поток газа входит с эксергией 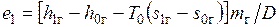 , а выходит с эксергией
, а выходит с эксергией 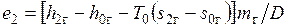 , теряя на килограмм пара эксергию
, теряя на килограмм пара эксергию 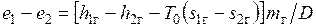 .
.
Соответственно увеличение эксергии килограмма пара 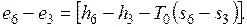 . Потери эксергии при передаче теплоты составят
. Потери эксергии при передаче теплоты составят
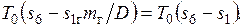
Графически эти потери изображаются заштрихованной на рис. 6.1 площадкой. Расчеты показывают, что только из-за неравновесного теплообмена потеря эксергии, т. е. работы, которую теоретически можно было бы получить, используя теплоту продуктов сгорания топлива, превышает 30%.
 2014-02-09
2014-02-09 2168
2168








