Ниже представлена таблица преобразования Лапласа для некоторых функций.
| № | Функция | Временная область 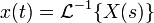
| Частотная область 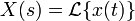
| Область сходимости для причинных систем |
| идеальное запаздывание | 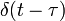
| 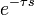
| ||
| 1a | единичный импульс | 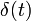
| 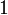
| 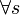
|
запаздывание 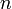 -го порядка с частотным сдвигом -го порядка с частотным сдвигом
| 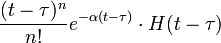
| 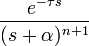
| 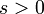
| |
| 2a | степенная 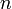 -го порядка -го порядка
| 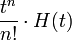
| 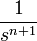
| 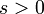
|
| 2a.1 | степенная 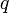 -го порядка -го порядка
| 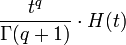
| 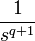
| 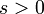
|
| 2a.2 | единичная функция | 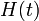
| 
| 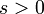
|
| 2b | единичная функция с запаздыванием | 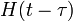
| 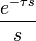
| 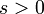
|
| 2c | «ступенька скорости» | 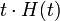
| 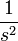
| 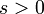
|
| 2d | 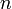 -го порядка с частотным сдвигом -го порядка с частотным сдвигом
| 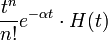
| 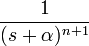
| 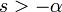
|
| 2d.1 | экспоненциальное затухание | 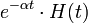
| 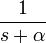
| 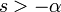
|
| экспоненциальное приближение | 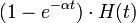
| 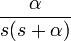
| 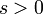
| |
| синус | 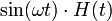
| 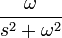
| 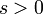
| |
| косинус | 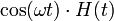
| 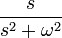
| 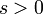
| |
| гиперболический синус | 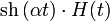
| 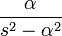
| 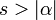
| |
| гиперболический косинус | 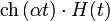
| 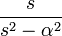
| 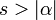
| |
| экспоненциально затухающий синус | 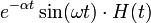
| 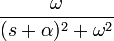
| 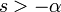
| |
| экспоненциально затухающий косинус | 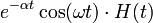
| 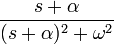
| 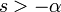
| |
корень 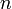 -го порядка -го порядка
| 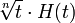
| 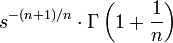
| 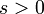
| |
| натуральный логарифм | 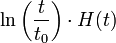
| 
| 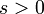
| |
функция Бесселя первого рода порядка 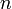
| 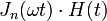
| 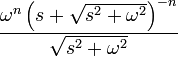
| 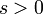 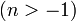
| |
модифицированная функция Бесселя первого рода порядка 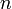
| 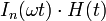
| 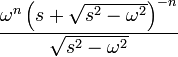
| 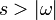
| |
| функция Бесселя второго рода нулевого порядка | 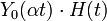
| 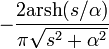
| 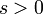
| |
| модифицированная функция Бесселя второго рода, нулевого порядка | 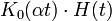
| |||
| функция ошибок | 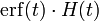
| 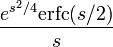
| 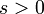
| |
Примечания к таблице:
|
 2014-02-09
2014-02-09 786
786

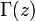 — гамма-функция;
— гамма-функция;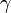 — постоянная Эйлера — Маскерони;
— постоянная Эйлера — Маскерони;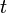 — вещественная переменная;
— вещественная переменная; — комплексная переменная;
— комплексная переменная;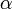 ,
, 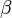 ,
, 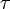 и
и 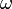 — вещественные числа;
— вещественные числа;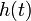 равна нулю для любого момента времени
равна нулю для любого момента времени 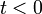 .
.






