СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ МАТЕМАТИКИ
Чувствительность и разрешающая способность МЭМП и НЭМП, источники помех (шума).
Эффективность микро- и нано- электромеханических преобразователей в целом и их отдельных элементов в решающей степени определяются их чувствительностью и разрешающей способностью. Чувствительность сенсорного элемента к внешнему воздействию характеризуется отношением абсолютной величины выходного сигнала как реакции на внешнее воздействие (ΔV) к величине внешнего воздействия (ΔF): SF=ΔV/ΔF. В случае актюаторного элемента ΔV соответствует величине входного сигнала, а ΔF – величине воздействия элемента на внешнюю среду. Разрешающая способность сенсорного элемента характеризуется минимальной величиной внешнего воздействия (ΔFmin), которая может быть детектирована, и определяется как отношение интенсивности помех, или шума (δVn) к чувствительности: δVn / SF=ΔFmin, или операционным пределом как отношением величины выходного сигнала как реакции на внешнее воздействие (ΔV) к интенсивности шума (δVn): R=ΔV /δVn. Разрешающая способность актюаторного элемента при этом характеризуется минимальной величиной активирующего воздействия (ΔFmin), которая может быть реализована актюатором, и определяется таким же соотношением: δVn / SF=ΔFmin. Операционный предел актюатора определяется отношением величины входного сигнала (ΔV) к интенсивности шума (δVn). Все эти характеристики часто в решающей степени зависят от схем усиления и регистрации сигналов и системы контроля и управления в целом, однако очень важный вклад в чувствительность, разрешающую способность МЕМП и НЭМП, применяемых в интеллектуальных конструкционных наноматериалах, и помехи в них вносят упругие механические элементы.
Чувствительность упругих механических элементов к действию силы или массы (веса) при квазистатических режимах, определяемая их способностью к деформации (деформативной податливостью) и оцениваемая отношением силы или массы к величине вызванной ими деформации, резко возрастает с уменьшением их размеров. Например для кремниевой консольной балки прямоугольного сечения сила, необходимая для прогиба конца балки на величину, равную ее толщине а, при ширине в=10а и длине l=100а, варьируется от 300 пиконьютонов (пН) при а =100 нм до 30 пН при а =10нм. Эти значения соответствуют весу отдельных молекул и лежат в интервале сил, необходимых для разрыва единичных межмолекулярных (комплексных лиганд-рецепторных и Ван-дер-ваальсовских) связей соответственно, если принять для первых энергию равной примерно 1 эВ (1,6х10-19 Дж), а для второй - 0,1 эВ при одинаковой их длине в 1нм. При динамических режима чувствительность механических упругих элементов, определяемая их способностью изменять (сдвигать) фундаментальную частоту при действии внешней силы или изменении массы, также резко возрастает с уменьшением размеров элементов. Так, для кремниевого балочного упругого элемента в виде кантилевера длиной 30 мкм, шириной 2 мкм и толщиной 500 нм с резонансной частой 375 кГц чувствительность к изменению массы составляет величину порядка 4х10-16 г/Гц.
Получение упругих элементов такого масштаба и чувствительности настоящее время возможно с использованием современных материалов и методов нанотехнологии. Однако, при этом становится очевидным, что чрезвычайно высокая чувствительность балочных элементов, особенно работающих в динамическом режиме, при переходе к наномасштабу может негативно сказываться на разрешающей способности МЭМП и НЭМП в целом вследствие резкого проявления фундаментальных побочных эффектов, вызывающих случайные колебания (флуктуации деформации – амплитуды или частоты, т.е. шум). Интенсивность таких случайных колебаний выражается через зависимые от частоты эффективные спектральные плотности мощности флуктуаций амплитуды Sz(ω) и частоты Sω(ω). Величина Sz(ω) с размерностью м2/Гц определяет средне-квадратичную мощность шума как отклонение амплитуды случайных колебаний от их среднего значения ‹(δz)2›=‹(z-‹z›)2› через ее интегрирование в соответствующей полосе измеряемых частот 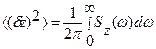 . Аналогичным образом Sω(ω) определяет среднеквадратичное отклонение фундаментальной, или собственной частоты в серии ее измерений
. Аналогичным образом Sω(ω) определяет среднеквадратичное отклонение фундаментальной, или собственной частоты в серии ее измерений 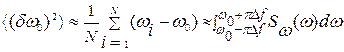 , где
, где 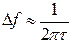 , τ - среднее время измерений. Угловые скобки указывают на усреднение по статистическому ансамблю. Чувствительность к амплитудным и частотным флуктуациям при этом оценивается как корень квадратный из Sx(ω) и Sω(ω) с размерностью мГц-1 \2 и Гц-1/ 2 соответственно.
, τ - среднее время измерений. Угловые скобки указывают на усреднение по статистическому ансамблю. Чувствительность к амплитудным и частотным флуктуациям при этом оценивается как корень квадратный из Sx(ω) и Sω(ω) с размерностью мГц-1 \2 и Гц-1/ 2 соответственно.
Основными источниками шума в упругих механических элементах, влияние которого на их разрешающую способность резко возрастает при переходе к наномасштабу, являются термомеханические и температурные флуктуации, а также эффекты адсорбции/десорбции молекул из окружающей среды.
А. Термомеханические флуктуации
Любая система, диссипирующая энергию, является источником шума. Верно и обратное утверждение. Эти основные положения являются следствием флуктуационно-диссипативной теоремы, согласно которой каждой моде колебаний в условиях термодинамического равновесия соответствует средняя энергия шума, равная 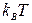 /2 для каждого квадратичного члена в выражении энергии для данной моды. Эта теорема хорошо известна применительно к электрическим цепям и носит название теоремы Нуйквиста-Джонсона. Флуктуационно-диссипативная теорема применима к механическим элементам с ненулевой диссипацией, т.е. с конечным значением Q- фактора. Однако, если такие флуктуации в электрических цепях заметно проявляются уже в макромасштабе, то в механических элементах они начинают заметно проявляться только в микро- и особенно резко в наномасштабе. Кроме того, из-за резонансной природы отклика механического осциллятора эта обычно теорема излагается в несколько иной форме. При этом считается, что термомеханические флуктуации являются следствием хаотического теплового (броуновского) движения в материале балочного элемента. В соответствие с этим энергия среднеквадратичных тепловых флуктуаций смещения центра масс упругой балки равна средней энергии теплового движения:
/2 для каждого квадратичного члена в выражении энергии для данной моды. Эта теорема хорошо известна применительно к электрическим цепям и носит название теоремы Нуйквиста-Джонсона. Флуктуационно-диссипативная теорема применима к механическим элементам с ненулевой диссипацией, т.е. с конечным значением Q- фактора. Однако, если такие флуктуации в электрических цепях заметно проявляются уже в макромасштабе, то в механических элементах они начинают заметно проявляться только в микро- и особенно резко в наномасштабе. Кроме того, из-за резонансной природы отклика механического осциллятора эта обычно теорема излагается в несколько иной форме. При этом считается, что термомеханические флуктуации являются следствием хаотического теплового (броуновского) движения в материале балочного элемента. В соответствие с этим энергия среднеквадратичных тепловых флуктуаций смещения центра масс упругой балки равна средней энергии теплового движения: 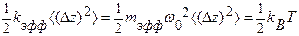 , откуда:
, откуда: 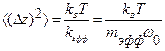 , где kB – константа Больцмана, Т - абсолютная температура. Эффективная спектральная плотность мощности амплитудных флуктуаций Sz(ω) с размерностью м2/Гц при этом равна:
, где kB – константа Больцмана, Т - абсолютная температура. Эффективная спектральная плотность мощности амплитудных флуктуаций Sz(ω) с размерностью м2/Гц при этом равна: 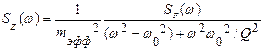 , где
, где 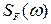 - эффективная спектральная плотность мощности флуктуаций термомеханических сил с размерностью н2/Гц:
- эффективная спектральная плотность мощности флуктуаций термомеханических сил с размерностью н2/Гц: 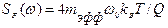 .
.
Эффективная спектральная плотность мощности флуктуаций частоты Sω(ω) определяется способом и условиями задания вынужденных колебаний механического резонатора. Если резонатор подвергается колебаниям с постоянной средне-квадратичной амплитудой 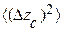 и максимальной энергией таких колебаний
и максимальной энергией таких колебаний 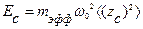 , то
, то 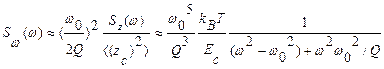 . Интегрирование этой величины в пределах от
. Интегрирование этой величины в пределах от 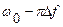 до
до 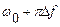 при условии, что Q>>1 и 2πΔf<<ω0/Q дает выражение для минимально детектируемого сдвига по частоте:
при условии, что Q>>1 и 2πΔf<<ω0/Q дает выражение для минимально детектируемого сдвига по частоте: 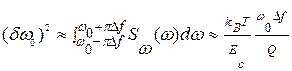 и чувствительности по массе:
и чувствительности по массе: 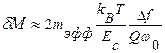 . При задании колебаний резонатора по схеме самовозбуждения:
. При задании колебаний резонатора по схеме самовозбуждения: 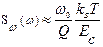 .
.
Большое значение при анализе спектра термомеханического шума микро- и нанорезонаторов имеет не только величина Q- фактора, но и механизм диссипации энергии и, соответственно, ее зависимость от температуры. При учете диссипации энергии только за счет внутреннего трения спектр шума как температурно-частотная зависимость средне-квадратичной амплитуды термомеханических колебаний описывается соотношением: 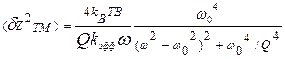 , где В – полоса частот измерений, kэфф –эффективная жесткость балки. При этом необходимо учитывать зависимость термоупругих диссипативных потерь от частоты. Например, показано, что для консольной балки толщиной а, плотностью ρ, теплопроводностью G и теплоемкостью C максимальная диссипация энергии проявляется при периодической частоте:
, где В – полоса частот измерений, kэфф –эффективная жесткость балки. При этом необходимо учитывать зависимость термоупругих диссипативных потерь от частоты. Например, показано, что для консольной балки толщиной а, плотностью ρ, теплопроводностью G и теплоемкостью C максимальная диссипация энергии проявляется при периодической частоте: 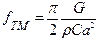 . Если основной вклад в демпфирование колебаний консольной балки оказывает вязкость окружающей среды, то спектр шума описывается соотношением:
. Если основной вклад в демпфирование колебаний консольной балки оказывает вязкость окружающей среды, то спектр шума описывается соотношением: 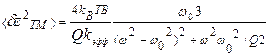 , из которого следует, что при частотах значительно меньше резонансной (ω<<ω0) и при частоте, равной резонансной (ω=ω0) спектр шума не зависит от частоты и описывается соотношениями, соответственно:
, из которого следует, что при частотах значительно меньше резонансной (ω<<ω0) и при частоте, равной резонансной (ω=ω0) спектр шума не зависит от частоты и описывается соотношениями, соответственно: 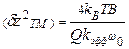 и
и 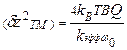 .
.
Б. Температурные флуктуации
Флуктуации температуры микро- и наномеханических чувствительных элементов, обусловленные их конечной теплопроводностью, могут вызывать изменения как геометрических размеров элементов, так и свойств материалов, из которых они изготовлены, и, соответственно, частотные флуктуации. Так, влияние температуры на коэффициент жесткости балки вследствие изменения ее геометрических размеров и модуля упругости материала можно описать уравнением: 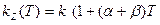 , где α и β – термические коэффициенты расширения и модуля упругости соответственно.
, где α и β – термические коэффициенты расширения и модуля упругости соответственно.
Для оценки эффективной спектральной плотности температурных флуктуаций и вызываемых ими частотных флуктуаций, была применена тепловая модель балки в виде некоторой теплоемкости С=сvV (сv – удельная теплоемкость материала; V - объем балки), соединенной теплопроводностью G=λl (λ – коэффициент теплопроводности материала; l- длина балки) с тепловым резервуаром с температурой Т. Средняя тепловая энергия системы, равная 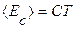 , флуктуирует в соответствие с флуктуационно- диссипативной теоремой аналогично термомеханическому шуму на среднюю величину δЕ с, со спектральной плотностью температурных флуктуаций
, флуктуирует в соответствие с флуктуационно- диссипативной теоремой аналогично термомеханическому шуму на среднюю величину δЕ с, со спектральной плотностью температурных флуктуаций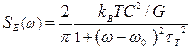 , где τт=С/G – время тепловой релаксации, или тепловая постоянная времени. Аналогичным выражением описывается спектральная плотность SТ(ω) флуктуацийтепловой энергии δЕ с, причем ее величина удваивается за счет учета неравномерной теплопроводности концов мостиковой структуры. Обобщенная оценка эффективной спектральной плотности флуктуаций частоты Sω(ω) для наномостиковой структуры длиной l дала следующий результат:
, где τт=С/G – время тепловой релаксации, или тепловая постоянная времени. Аналогичным выражением описывается спектральная плотность SТ(ω) флуктуацийтепловой энергии δЕ с, причем ее величина удваивается за счет учета неравномерной теплопроводности концов мостиковой структуры. Обобщенная оценка эффективной спектральной плотности флуктуаций частоты Sω(ω) для наномостиковой структуры длиной l дала следующий результат: 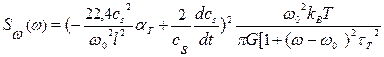 , где
, где 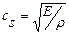 - зависимая от температуры скорость звука; αт – линейный термический коэффициент расширения,
- зависимая от температуры скорость звука; αт – линейный термический коэффициент расширения, 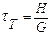 - тепловая постоянная времени, или характерное время тепловой релаксации, G и Н – теплопроводность и теплоемкость структуры соответственно. Выражение для минимально детектируемого сдвига по частоте имеет при этом вид:
- тепловая постоянная времени, или характерное время тепловой релаксации, G и Н – теплопроводность и теплоемкость структуры соответственно. Выражение для минимально детектируемого сдвига по частоте имеет при этом вид: 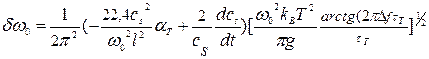
и чувствительности по массе [24]: 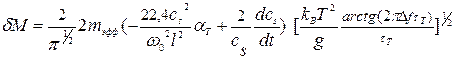 .
.
В. Эффекты адсорбции/десорбции молекул из окружающей среды
Адсорбция молекул газов из окружающей среды массой М, изменяя эффективную массу наноструктуры, сдвигает ее резонансную частоту. Следовательно, случайные, термически обусловленные процессы адсорбции и десорбции молекул с конечной энергией их связей при ненулевой температуре, должны вызывать частотные флуктуации и быть источником фазово-частотного шума, принципиально отличного от шума, вызываемого диссипацией упругой энергии. При этом сдвиг фундаментальной частоты должен быть пропорционален отношению М/mэфф и, следовательно, с уменьшением массы резонатора его чувствительность к процессам адсорбции/десорбции должна увеличиваться. Кроме того, с уменьшением размера резонатора отношение числа активных мест на его поверхности к общему числу атомов в нем возрастает, что еще больше увеличивает чувствительность структур наномасштаба к этому эффекту.
Таким образом, высокая чувствительность упругих элементов к механическим смещениям, многообразие источников шума в них, указанных выше, и его высокая интенсивность в микро- и наномасштабе могут оказывать значительное влияние на чувствительность и разрешающую способность детекторных и актюаторных МЭМП и НЭМП. Сами детекторные и актюаторные элементы также могут быть источником шума вследствие электрических процессов, протекающих непосредственно в системе и в схемах усиления и контроля. Анализ физических принципов и закономерностей работы основных элементов электромеханических преобразователей, побочных эффектов и явлений в них показывает, что при переходе от микро- к наномасштабу проблемы создания чувствительных упругих элементов и их активации с заданием очень малых смещений с высокой точностью и частотой могут быть достаточно эффективно решены с помощью самых современных материалов и процессов твердотельной нанотехнологии. Однако, детектирование таких смещений остается очень сложной и далеко еще нерешенной задачей. Решение этой задачи требует достижения беспрецедентно высокого уровня точности фиксирования и разрешения наносмещений при очень высоких рабочих частотах. Поэтому в настоящее время в области исследований и разработок МЭМП и НЭМП, в том числе применительно к интеллектуальным конструкционным наноматериалам, наибольшее внимание уделяется созданию высокочувствительных, широкополосных, работоспособных и надежных детекторов электромеханических преобразователей с использованием самых современных («умных») материалов и технологий.
(Теория вероятностей и математическая статистика)
 2014-02-09
2014-02-09 875
875







