Лекция №9. Определение принадлежности крайних вариант к совокупности

Определение принадлежности крайних вариант к совокупности.

Основным требованием при математической обработке опытных данных является сохранение всех этих данных. Однако, нередко бывает так, что крайние варианты слишком значительно отличаются от среднего значения. Такие крайние варианты могут быть результатом грубых ошибок в оценке времени и поэтому должны быть исключены из выборки.

Очевидно, что при отбрасывании крайних вариант следует исходить не из субъективных рассуждений исследователя, а из научного анализа данных ряда распределения.

Существует несколько методов определения принадлежности крайних вариант к совокупности. Наиболее часто применяемым методом является метод, основанный на применении таблицы значений интеграла вероятностей. В этом случае априори полагают наличие нормального закона распределения для полученной выборки. В нашем случае имеется косвенное подтверждение наличия нормального закона. Полагаем, что параметры нормального распределения равны: 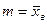и 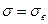. Выбираем одну из крайних вариант, например, наибольшую по своей величине варианту t_k и определяем вероятность попадания случайной точки в два симметрично расположенные относительно математического ожидания промежутка числовой оси 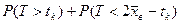. На приведенном ниже рисунке эти промежутки соответствуют заштрихованным зонам под графиком плотности нормального распределения, а сама вероятность численно равна сумме площадей заштрихованных зон. Удобно искомую вероятность определять через вероятность противоположного события – вероятность непопадания в выделенные промежутки числовой оси. С учётом того, что вся площадь под кривой плотности численно равана единице и кривая – симметричная относительно вертикальной оси 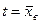, то интеграл вычисляем по половине области интегрирования.

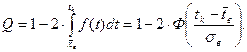
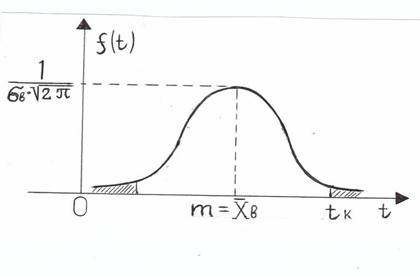
Если найденная вероятность окажется практически малой (меньше 0,05), то рассматриваемое крайнее значение варианты может быть отброшено, т. е. исключено из выборки, и не учитываться в дальнейших исследованиях.

Определим принадлежность крайних вариант к одной и той же генеральной совокупности, считая 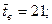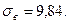Расчёт выполняем с помощью таблицы 6.

Таблица 6.

№ п. п.	Крайняя варианта tk		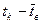		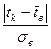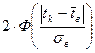Q	Заключение
		-15	1,52	0,8715	0,1185	Q>0,05
			3,76	0,9998	0,0002	Q<0,05
			3,25	0,9989	0,0011	Q<0,05
			2,44	0,9853	0,0147	Q<0,05
			2,24	0,9749	0,0251	Q<0,05
			1,93	0,9464	0,0536	Q>0,05

Вывод. Варианты 43 (повторяется два раза), 45, 53 и 58 необходимо из выборки исключить как маловероятные.

Для больших выборок простейшим критерием для исключения вариант из совокупности может служить правило «трёх сигм»: если выполняется неравенство 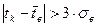, то варианта t_k может быть исключена из выборки.

Определение параметров «очищеной» выборки.

Для определения среднего выборочного и дисперсии «очищеной» выборки необходимо заново построить интервальный вариационный ряд, удовлетворяющий ранене сформулированными требованиями.

Число интервалов определяем по формуле: 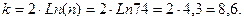В целях избежания малочисленных вариант принимаем к=5. Интервальный ряд для «очищеной» выборки приведен в таблице 7. При составлении таблицы принимали h = 7 минут (временная протяжённость интерваплов) и С = 16 – «ложный» нуль.

Таблица 7.

Интервалы	Середины Интервалов ti	Частота ni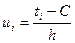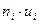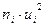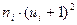
5,5 – 12,5			-1	-10
12,5 -19,5
19,5 -26,5
26,5 – 33,5
33,5 – 40,5

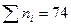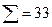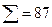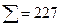Проверка правильности вычислений: 66 + 87 + 74 = 227, т. е. расчёт выполнен верно.

;

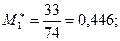
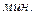
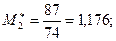
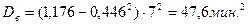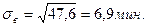
Статистическая проверка статистической гипотезы о

наличии нормального закона распределения.

Статистическую проверку гипотезы о наличии нормального закона распределения для исследуемой генеральной совокупности осуществим при помощи критериев согласия Пирсона и Романовского. С этой целью построим теоретическую кривую по выравнивающим частотам для нормального закона и сравним её с полигоном наблюдённых частот.

Будем определять выравнивающие частоты (т. е. ординаты теоретической кривой) по формуле, вытекающей из определения статистической плотности вероятности, которая строится по интервальному статистическому вариационному ряду. Статистической плотностью вероятности 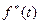называется функция, значение которой на каждом интервале 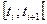постоянны и равны относительной частоте события 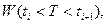поделённой на длину интервала 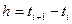, т. е.

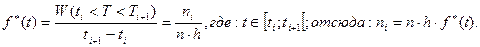
Ступенчатый график статистической плотности вероятности называется гистограммой.

Заменяя в последней формуле функцию 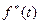на нормированную функцию распределения для нормального закона, получим выражение для подсчёта выравнивающей (теоретической) частоты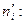

;

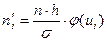Здесь: n – сумма наблюдённых частот;

h – величина интервала ряда;

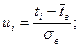
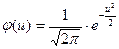- нормированная функция плотности распре- деления вероятностей нормального закона. Значения функции берутся из таблицы (см. приложение, таблица 1). Входом в таблицу служат рассчитанные .

Следует иметь ввиду, что сумма выравнивающих (теоретических) частот должна быть равна сумме наблюдённых. Результат расчёта приведен в таблице 8.

При расчёте было принято: n = 74;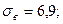

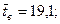
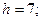
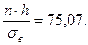
Таблица 8.

Середина интервала	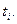Наблюдённые частоты			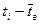	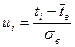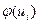Выравнивающ. частоты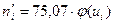
		-17,1	-2,4783	0,0184	1,38
		-10,1	-1,4638	0,1374	10,31
		-3,1	-0,4493	0,3605	27,06
		3,9	0,5652	0,3400	25,52
		10,9	1,5797	0,1163	8,73
		17,9	2,5942	0,0140	1,051

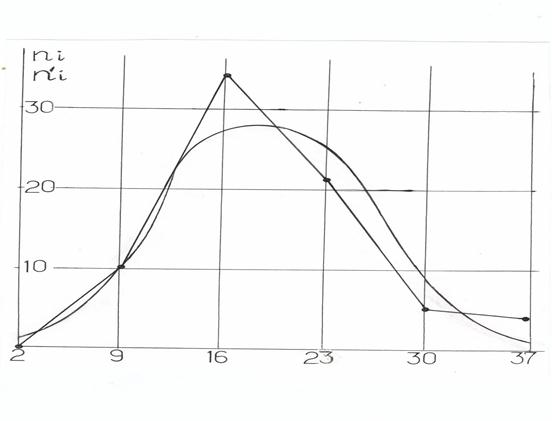
По данным таблицы 8 в прямоугольной системе координат строим точк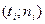и и 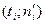, соединяя первые отрезками прямых, а вторые (теоретические) – плавной кривой. Сравнивая графики (см. ниже), можно сделать вывод о том, что выравнивающие и наблюдённые частоты не сильно отличаются друг от друга, т. е. распределение оценок времени близко к теоретическому, построенному для нормального закона распределения. Однако, чтобы уверенно сказать, что данные эксперимента соответствуют нормальному распределению, следует применить более строгие, надёжные количественные оценки. Такие количественные оценки называют критериями согласия.

Эти критерии позволяют судить о согласовании данныъх наблюдений с выдвинутой статистической гипотезой о наличии нормального закона распределения.

Анализ кумулятивного графика в соответствии с правилом одного, двух и трёх «сигм», построенного по данным таблицы 5, позволил нам выдвинуть гипотезу о наличии нормального распределения в полученной выборке. Эта гипотеза была использована при вычислении выравнивающих частот, которые, как видно из графика (см. ниже), не совпадают с наблюдёнными.

Вполне логичен вопрос, является ли расхождение между выравнивающими и наблюдёнными частотами случайным или значимым, т. е. реальными? Если расхождение окажется случайным, то можно сказать, что данные выборки согласуются с выдвинутой гипотезой и, следовательно, гипотезу можно принять. Если же расхождение окажется значимым, то данные выборки не согласуются с гипотезой и её следует отвергнуть.

Имеется несколько критериев согласия, в настоящем кратком курсе ограничимся описанием только двух: критерия Пирсона («хи – квадрат») и критерия Романовского.

В случае применения критерия Пирсона вычисляется сумма квадратов разностей между наблюдёнными и выравнивающими частотами, отнесённых к величинам выравнивающих частот:

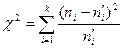, здесь: k – число интервалов.

Из формулы видно, что чем больше согласуются эмпирическое и теоретическое распределения, тем меньше будет разность 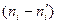и, следовательно, тем меньше будет критерий .

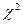Таким образом, критерий 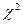в известной степени характеризует близость эмпирического и теоретического распределений. Имеются специальные таблицы, в которых указана вероятность того, что, в результате влияния случайных факторов, величина критерия 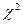примет значение не меньшее, чем вычисленное по данным выборки число, обозначенное как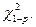

Входом в таблицу является уровень значимости (величина вероятности, которую можно считать малой) и число степеней свободы. Для нормального закона число степеней свободы f определяется по формуле: f = k – 3, где k – число интервалов ряда.

В качестве границы между случайным и существенным выбираем, например, 5% - ный уровень значимости. Если вероятность 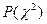будет меньше 0,05, то наблюдённое значение 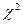считается не случайным, так как событие с такой малой вероятностью полагается практически невозможным. В таком случае расхождение между гипотезой и наблюдёнными данными тоже надо считать не случайным, а существенным. Следовательно, малая вероятность 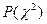указывает на недостаточное согласие между гипотезой и наблюдениями. Если же вероятность 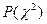будет больше 0,05, то расхождение между гипотезой и эмпирическими данными можно считать случайным, а саму гипотезу считать согласующейся с наблюдениями.

На практике обычно не определяют вероятность 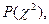а сравнивают найденное 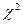и табличное 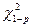(см. приложение, таблица 2). Если 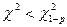, то гипотеза не отвергается. Если же 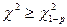, то гипотезу о нормальном законе распределения следует отвергнуть.

При использовании критерия Пирсона требуется, чтобы в каждом интервале было не меньше 5 наблюдений. Если это условие не выполнено, необходимо частоты крайних интервалов объединить между собой. Расчёт критерия 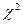приведен в таблице 9. Для её построения использованы данные таблицы 8. Теоретические (выравнивающие) частоты округлены до целых значений.

Таблица 9.

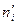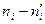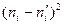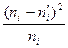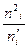		-1		0,09	9,09
				1,81	42,81
		-5		0,97	16,96
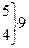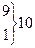		-1		0,1	8,1

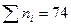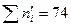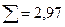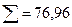Проверку правильности при вычислении критерия 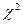необходимо проводить по формуле:

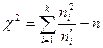, где n – объём выборки.

Проверка: 76,96 – 74 = 2,96, т. е. значение критерия вычислено верно.

По таблице значений 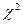(см. приложение, таблица 2) для числа степеней свободы f =4 – 3 = 1 и уровня значимости 0,05 находим критическое значение критерия 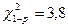. Так как 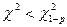, то гипотезу о нормальном распределении генеральной совокупности следует считать правильной.

Критерий Романовского состоит в следующем: если выполняется неравенство

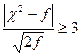
То расхождение между эмпирическим и теоретическим распределениями можно считать существенным. Если знак неравенства – противоположный, то расхождение можно считать случайным.

В нашем случае 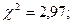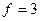. Поэтому 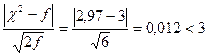, т. е. расхождение носит случайный характер.

Итак, справедливость выдвинутой гипотезы подтверждается двумя критериями и сравнением графиков наблюдённых и выравнивающих частот.

Доверительные границы для среднего выборочного совокупности.

Для получения представлеения о точности и надёжности какого либо параметра распределения в полученной выборке, в математической статистике используют доверительный интервапл и доверительную вероятность.

Пусть в результате обработки опытных данных получена точечная оценка, например, среднего выборочного 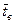. Как оценить возможную при этом ошибку?

Поступают следующим образом.

- Назначается вероятность 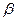из числа значений 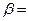0,9; 0,95; 0,99 такую, что событие с вероятностью 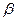можно считать практически достоверным.

- Находится такое значение 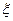, для которого вероятность неравенства

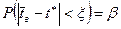, т. е. практически возможная ошибка по абсолютной величине не превосходит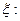 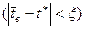. Здесь 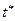- неизвестное точное значение среднего выборочного (величина не случайная). Перейдём от модульного неравенства под знаком вероятности Р к двойному безмодульному:

.

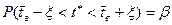Геометрическая интерпретация выражения такова: неслучайная величина 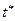с вероятностью 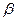«накрывается» интервалом 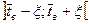, границы которого - случайны. Точнее, случаен центр интервала 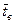, определяющий положение интервала на числовой оси, случайна и длина интервала.

Вероятность 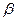называется доверительной вероятностью;

Интервал, «накрывающий» с вероятностью 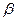неизвестное точное значение 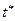среднего выборочного, называется доверительным интервалом, а его границы – доверительными границами.

На практике задача определения доверительного интервала при заданной доверительной вероятности решается как приближёнными, так и точными методами. Приближённый метод даёт удовлетворительные по точности результаты, если имеется сравнительно большое число опытов (n > 20). В нашем случае вполне применим приближённый метод.

Суть метода заключается в замене в выражении для 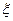неизвестных параметров 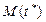и 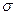их точечными оценками. Так как среднее выборочное есть сумма n независимых, одинаково распределённых случайных величин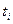 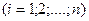(результат каждого наблюдения рассматриваем как случайную величину) 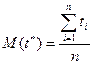, то при достаточно большом n её закон распределения близок к нормальному. Следовательно, согласно центральной предельной теореме, случайная величина 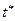распределена по нормальному закону с параметрам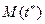и и 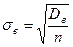. Тогда вероятность двойного неравенства может быть выражена через нормированную функцию распределения для нормального закона:

.

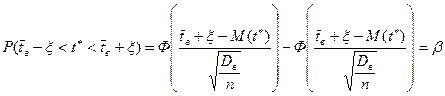Полагая в последнем выражении 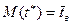, получим:

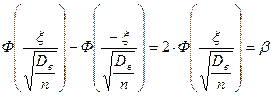, откуда: .

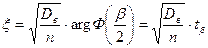Величину 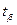находим для выбранной доверительной вероятности 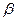по таблице 1 приложения.

Итак, доверительный интервал равен: .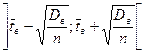

Если принять доверительную вероятность 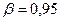, то с принятой вероятностью можно утверждать, что неизвестное срднее значение генеральной совокупности 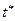лежит между числами:

.

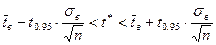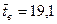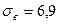Принимая n = 74, и , по таблице 1 находим .

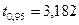Тогда: .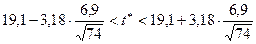

Или: .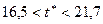

Порядок работы с выборкой объёма n > 30 может быть следующим.

1. Составляем сводку данных.

2. Составляем интервальный ряд с последующим определением выборочного среднего, дисперсии и стандарта.

3. Строим кумулятивный график, по правилу одного, двух и трёх «сигм» проверяем возможность выдвижения гипотезы о наличии нормального закона распределения выборки.

4. Исключаем из выборки маловероятные варианты.

5. Рассчитываем выборочное среднее, дисперсию и стандарт для «очищенной» выборки.

6. Рассчитываем выравнивающие (теоретические) частоты и строим график наблюдённых и выравнивающих частот.

7. Проверяем согласование данных выборки с выдвинутой гипотезой.

8. Определяем доверительные границы для среднего выборочного.