Решение об объеме выборки является компромиссом между теоретическими предположениями о точности результатов обследования и возможностями их практической реализации. Известно, что чем больше объем выборки, тем меньше ее ошибка. Однако необходимо учитывать, что, стоимость выборки растет пропорционально ее объему, а ошибка выборки уменьшается по норме, равной квадратному корню из относительного роста размера выборки. Если размер выборки увеличить в 4 раза, то ошибка выборки уменьшится только на половину.
Оптимальный объём выборки зависит от следующих параметров:
- типа выборки;
- изучаемых характеристик и их распределения в генеральной совокупности;
- доступных ресурсов (финансовых, временных) для исследования.
Подходы к определению объема выборки.
Произвольный подход основан на применении «правила большого пальца». Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5% от генеральной совокупности.
Объем выборки может быть установлен исходя из некоторых заранее оговоренных условий. При изучении общественного мнения выборка обычно составляет 1000-1200 человек.
В случае, если на каком-то рынке проводятся ежегодные исследования, то в каждом году используется выборка одного и того же объема.
Выборка при проведении исследования предпочтений целевой аудитории - 160-300 человек.
Объем выборки может определяться на основе статистического анализа. Этот подход основан на определении минимального объема выборки исходя из требований к надежности и достоверности получаемых результатов.
В математической теории выборочного наблюдения доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются (чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Принципиальную возможность определения генеральной средней по данным простой случайной выборки доказывает теорема П.Л. Чебышева, также известная как «закон больших чисел». В приложении к выборочному методу неравенство. П.Л. Чебышева может быть сформулировано так: при неограниченном, увеличении числа независимых наблюдений в генеральной совокупности с ограниченной дисперсией с вероятностью, сколь угодно близкой к единице, можно ожидать, что отклонение выборочной средней от генеральной средней будет сколь угодно мало.
Центральная предельная теорема А. М. Ляпунова, доказана в 1901 г. Согласно этой теореме, при достаточно большом числе независимых наблюдений и генеральной совокупности с конечной средней и ограниченной дисперсией вероятность того, что расхождение между выборочной и генеральной средней \х~-х\ не превзойдет по абсолютной величине, некоторую величину, равна интегралу Лапласа.
Разделяют два типа ошибок (случайная и систематическая). Случайная (статистическая) ошибка - это такие ошибки, которые возникают вследствие случайной вариации значений, вызванной тем, что наблюдается только часть единиц, а не вся ГС. Случайные ошибки уменьшаются с увеличением объема ВС. Случайную ошибку можно измерить методами математической статистики, если при формировании ВС соблюдался принцип случайности.
Для соблюдения принципа случайности формирование выборочной совокупности должно проходить по строго определенным правилам, которые составляют суть методов формирования выборочной совокупности. На практике принцип случайности соблюсти очень сложно, а иногда просто невозможно, что приводит к появлению систематической ошибки. Систематическая ошибка - это неконтролируемые перекосы в распределении выборочных наблюдений. Число опрошенных не влияет на величину систематической ошибки.
Нормальное распределение на графике выглядит как непрерывная кривая. Площадь, ограниченная этой кривой над любым заданным отрезком оси х, равна частоте или вероятности попадания случайного числа на этот отрезок.

 |
Среднее арифметическое находится при помощи усреднения, т.е. сложения данных и деления полученного результата на количество слагаемых.
Понятие вариации характеризует величину несхожести (схожести) ответов респондентов на определенный вопрос. В качестве меры вариации обычно принимается среднее квадратическое отклонение, которое характеризует среднее расстояние от средней оценки ответов каждого респондента на определенный вопрос.
При определении объёма выборки исследователь использует два основных статистических параметра: точность оценки и степень достоверности оценки.
Точность оценки – величина ошибки результата в абсолютном или относительном выражении. Степень достоверности оценки – вероятность того, что оценка соответствует истинному значению при установленной точности, т.е. вероятность гарантирующая результат.
Доверительный интервал – интервал, в который попадает определенный процент выборочных средних.
Из свойств нормальной кривой распределения вытекает, что конечные точки доверительного интервала, равного скажем 95%, определяются как произведение 1,96, называемого нормированным отклонением, на среднее квадратическое отклонение. Числа 1,96 и 2,58 (для 99%-ного доверительного интервала) обозначаются как z. Имеются таблицы «Значения интеграла вероятностей», которые дают возможность определить величины z для различных доверительных интервалов. Доверительный интервал, равный или 95%, или 99%, является стандартным при проведении маркетинговых исследований.
Значение нормированного отклонения оценки (z) от среднего значения в зависимости от доверительной вероятности (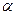 ) полученного результата.
) полученного результата.
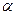 , % , % | 99,7 | ||||||||
| z | 0,84 | 1,03 | 1,29 | 1,44 | 1,65 | 1,96 | 2,18 | 2,58 | 3,0 |
В общем случае, для выборок достаточно большого объёма (больше 30 элементов) при оценке уровня среднего значения признака в генеральной совокупности, объём определяется по следующей формуле:
| При индивидуальном повторном отборе d2 z 2 n = ¾ e2 | При индивидуальном бесповторном отборе d2 z 2 N n =------------- Ne2+ z 2d2 |
где:
n – объём выборки;
z – нормированное отклонение, соответствующее принятому уровню доверительной вероятности (то есть вероятности, с которой истинное значение признака в генеральной совокупности будет соответствовать значению признака в выборочной совокупности), определяется по статистическим таблицам;
e2 – предельная ошибка выборки (то есть величина, устанавливающая границы интервала относительно выборочного среднего значения, в которые с указанной доверительной вероятностью попадёт генеральное среднее значение изучаемого признака);
σ² - дисперсия исследуемого признака в генеральной совокупности;
N – объем генеральной совокупности
При любом виде проектируемой выборки расчет ее объема производят по формуле повторного отбора. Если доля последнего превысит 5 % от генеральной совокупности, то переходят к расчету по формуле бесповторного отбора. Если доля выборочной совокупности будет меньше 5 %, то к формуле бесповторного отбора не переходят, т.к. это существенно не скажется на величине выборки.
Величина σ² зачастую бывает неизвестна, поэтому используют приближенные способы ее оценки:
- можно провести так называемое пробное маркетинговое исследование (небольшого объема), на базе которого и определяется величина дисперсии признака;
- можно использовать данные прошлых выборочных обследований. Если структура и условия развития явления достаточно стабильны, то σ "1/3 Х;
- если распределение признака в генеральной совокупности подчиняется нормальному закону, то размах вариации приблизительно равен 6σ (крайние значения отстоят в ту и другую сторону от средней на расстояние 3σ, т.е. σ = 1/6 (Х max - X min);
- для относительной величины признака принимают максимальную величину дисперсии σ² = 0,5 * 0,5 = 0,25.
Возможно определение объема выборки на основе процентных величин. Например, исследуется мнение потребителей о новом продукте и заказчик данного исследования указал, что его устроит точность полученных результатов, равная 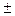 5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25% – 35%. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.
5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25% – 35%. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.
Когда на исходный вопрос существует только два варианта ответа, выраженное в % (например, 30% респондентов будет покупать новый продукт, а 70% не будет покупать новый продукт), объем выборки определяется по следующей формуле:
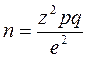 ,
,
где n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности;
р – найденная вариация для выборки;
q = (100 – p);
e – допустимая ошибка.
При использовании процентной меры изменчивости принимается в расчет то обстоятельство, что максимальная изменчивость достигается для p = 50%, что является наихудшим случаем. Иногда, когда невозможно определить вариацию для выборки используют максимальную меру изменчивости.
Приведенные формулы расчета объема выборки основаны на предположении, что все правила формирования выборки были соблюдены и единственной ошибкой выборки является ошибка, обусловленная ее объемом. Однако, следует помнить, что объем выборки определяет точность полученных результатов, но не их представительность, которая определяется методом формирования выборки.
1. В ходе исследования запланировано выяснить отношение жителей города Воронежа к новому продукту – соль диетическая. Предварительные данные отсутствуют. Необходимо определить объем выборки для поквартирного опроса методом личного интервью. Заказчика устроит уровень доверительной вероятности, равный 95%, если ошибка будет составлять не более 3%.
Применим формулу:
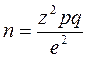 ,
,
где n – размер выборки;
z = 1,96 - значение нормированного отклонения оценки от среднего значения при уровне доверительной вероятности 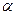 =95%;
=95%;
р = 50% - поскольку нет предварительных данных, предполагаем наихудший вариант разброса ответов;
q = (100 – p) = 50%;
e = 3% - допустимая ошибка.
Получаем: n = 1067.
2. Количество предприятий, использующих в своем производстве конвейерную ленту общего назначения, составляет 2300. Доля предприятий, предпочитающих импортную ленту, по предварительным данным составляет около 20%. При величине доверительной вероятности 95% найти объем выборки, если ошибка должна составить не более 5%.
Применим формулу:
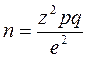 ,
,
где n – размер выборки;
z = 1,96 - значение нормированного отклонения оценки от среднего значения при уровне доверительной вероятности 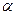 =95%;
=95%;
р = 17% - найденная вариация для выборки;
q = (100 – p) = 83%;
e = 5% - допустимая ошибка.
Получаем: n = 217.
Поскольку генеральную совокупность можно считать малой, то скорректируем полученное значение объема выборки по формуле:

Подставляя в формулу имеющиеся значения, получаем n’ = 207.
Допустим, что для обследования мнений потребителей о новом товаре – стиральном порошке "Ланца" - необходимо провести анкетирование. В районе насчитывается 10 тыс. семей. Условно принимается, что в одной квартире живет одна семья и на нее будет выделена одна анкета. Предварительные расчеты показали, что средне квадратичное отклонение размера покупки составляет 24; предельная ошибка не должна превышать 0,5 руб.
d2 z 2 N
n =-------------
Ne2 + z 2d2
Для того, чтобы гарантировать результат с вероятностью 95,4 % (z = 2), необходимо обследовать 370 семей. Эту величину можно округлить до 400 семей, т.е. устанавливается 4 % выборка.
Условные обозначения для переменных генеральной совокупности.
| Переменная | Генеральная совокупность | Выборка |
| Среднее | µ | X |
| Доля | π | p |
| Дисперсия | σ2 | s2 |
| Среднеквадратичное (стандартное) отклонение | σ | s |
| Объем | N | n |
| Стандартная ошибка среднего | σx | Sx |
| Стандартная ошибка доли | σp | Sp |
| Нормированное отклонение (z) | X - µ σ | _ X - X s |
| Коэффициент вариации | σ µ | S X |
Формула расчета дисперсии:
σ2 = Σ (хi – х)2
n - 1
Стандартная ошибка среднего (доли) относится к выборочному распределению среднего или доли, а не к выборке или всей совокупности.
σx = __ σ __
√ n
σx = √ __ σ __
n
Нормированное отклонение z точки – это количество стандартных ошибок, на которые точка удалена от среднего.
z = __ X - µ__
σx
Zi = (Xi-X)/Sx
Ошибка, степень точности – максимально допустимое различие между выборочным средним и генеральным средним.
Нормальное распределение – симметричный график, колоколообразная форма. Функция нормального распределения задается генеральным средним µ и генеральным стандартным отклонением σ. Существует бесконечное множество комбинаций µ и σ.
Расчет средней ошибки повторной простой случайной выборки производится следующим образом:
cредняя ошибка для средней:
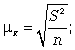
cредняя ошибка для доли:
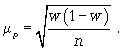
Расчет средней ошибки бесповторной случайной выборки:
средняя ошибка для средней:
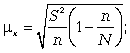
средняя ошибка для доли:
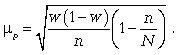
Расчет предельной ошибки 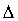 повторной случайной выборки:
повторной случайной выборки:
предельная ошибка для средней:
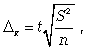
предельная ошибка для доли:
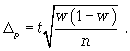
где t - коэффициент кратности;
Расчет предельной ошибки бесповторной случайной выборки:
предельная ошибка для средней:
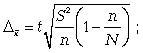
предельная ошибка для доли:
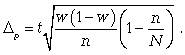
 2014-02-02
2014-02-02 40497
40497
