Вероятность отклонения относительной частоты события А от его теоретической вероятности

Пусть проведено n независимых испытаний и в т из них событие А появилось. Относительная частота появления события 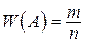. Теоретическая вероятность появления события А в каждом из n независимых испытаний равна р.

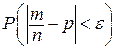Требуется найти , где e – заданное число. Событие 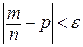запишем по-другому: 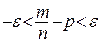или 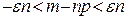. Отсюда 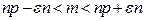. Используя интегральную формулу Лапласа, найдем требуемую вероятность: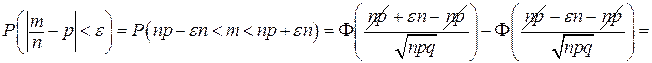

.

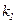
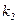
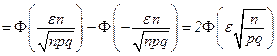Итак: .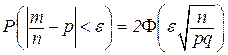

Пример: Вероятность того, что деталь нестандартна, равна р = 0,1. Найти, какое количество деталей надо отобрать, чтобы с вероятностью р = 0,9544 можно было утверждать, что относительная частота появления нестандартных деталей среди отобранных отклонится от постоянной вероятности р по абсолютной величине, не более чем на 0,03.

р = 0,1; e = 0,03; Р = 0,9544;. n -? q = 0,9.

.

; .

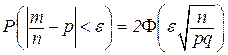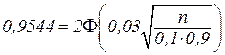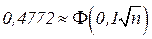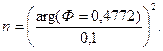
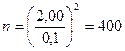деталей.