Рассмотрим последовательность 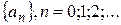
Определение. Последовательность 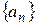 называется возвратной, если для некоторого k и всех n выполняется соотношение вида
называется возвратной, если для некоторого k и всех n выполняется соотношение вида
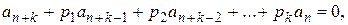 (13)
(13)
где постоянные коэффициенты pi;i=1;2;…;k не зависят от n.
Многочлен 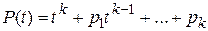 (14)
(14)
называется характеристическим многочленом для возвратной последовательности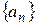 .
.
Соотношение 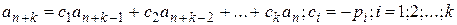 (15)
(15)
называют однородным линейным рекуррентным соотношением.
Из формулы (15) найдем общий член 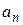 , для этого достаточно найти производящую функцию последовательности
, для этого достаточно найти производящую функцию последовательности 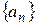 - функцию
- функцию 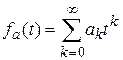 . Введем вспомогательный многочлен
. Введем вспомогательный многочлен 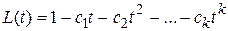 и рассмотрим произведение
и рассмотрим произведение 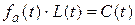 , при этом степень С(t) не превышает k-1, поскольку коэффициенты при tn+k ,k=0;1;… будут равны нулю в силу уравнения (15). Пусть характеристическое уравнение (14) имеет простые (может быть кратные) корни, т.е. допускает разложение вида
, при этом степень С(t) не превышает k-1, поскольку коэффициенты при tn+k ,k=0;1;… будут равны нулю в силу уравнения (15). Пусть характеристическое уравнение (14) имеет простые (может быть кратные) корни, т.е. допускает разложение вида 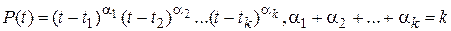 . Тогда
. Тогда 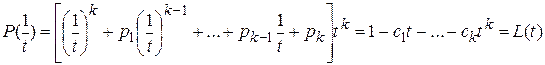 ,
,
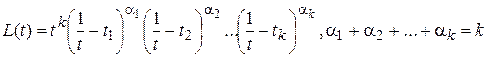 .
.
Характеристическую функцию можно представить в виде
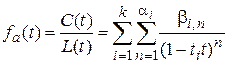 (16)
(16)
Известно, что  , то
, то 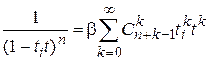 , и, следовательно,
, и, следовательно, 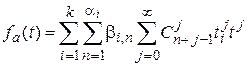 . (17)
. (17)
Формула (17) дает разложение производящей функции последовательности 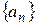 . Для нахождения формулы общего члена
. Для нахождения формулы общего члена 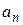 необходимо найти коэффициенты при tn в разложении (17).
необходимо найти коэффициенты при tn в разложении (17).
Пример1. Найти общий член последовательности 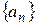 , удовлетворяющей рекуррентному соотношению
, удовлетворяющей рекуррентному соотношению 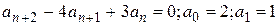 .
.
Решение. Перепишем исходное рекуррентное соотношение в виде (15)
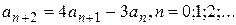
Характеристический многочлен L(t) имеет вид 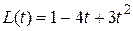 , тогда
, тогда
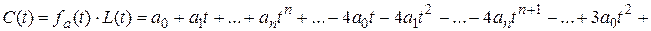
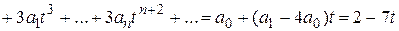 ,
,
Т.к. 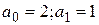 тогда
тогда 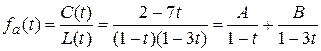 .
.
Методом неопределенных коэффициентов получим
получим
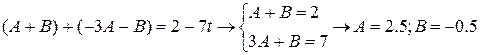
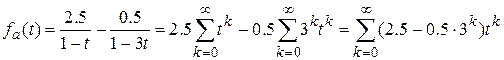 .
.
Способы нахождения общего решения рекуррентных соотношений:
1. Если возвратная последовательность (13) полностью определяетсязаданием еепервых k членов, то
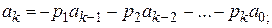
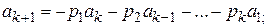
…………………………………….
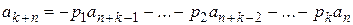 .
.
2. Если t является корнем характеристического многочлена (14), то последова- тельность {tn} удовлетворяет соотношению (13), тогда 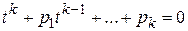 .
.
3. Если t1;t2;…;tk простые (некратные) корни характеристического многочлена(14), тогда общее решение рекуррентного соотношения (13) имеет вид
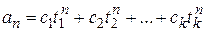 , (18)
, (18)
где с1;с2;…;ск – подходящие константы.
4. Если 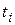 есть корень многочлена (14) кратности
есть корень многочлена (14) кратности 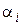 , то общее решение рекуррентного соотношения (13) имеет вид
, то общее решение рекуррентного соотношения (13) имеет вид
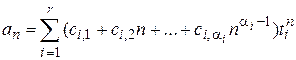 , (19)
, (19)
где сi,j=1;2;…;r; j=1;…;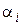 - произвольные константы, r – количество кратных корней.
- произвольные константы, r – количество кратных корней.
Пример 2. Найти общее решение для примера 1.
Решение. Характеристический многочлен 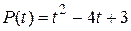 имеет корни t1=1; t2=3, тогда по формуле (18) получим
имеет корни t1=1; t2=3, тогда по формуле (18) получим 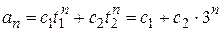 .
.
Пример 3. Решить неоднородное рекуррентное соотношение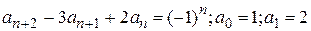 .
.
 2014-02-09
2014-02-09 5890
5890
