Решение.
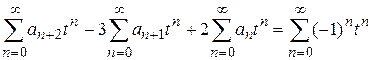 ,
,
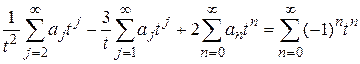 ,
,
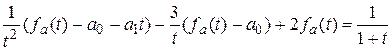 ,
,
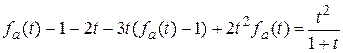 ,
,
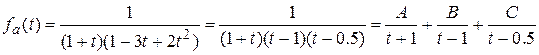 ,
,
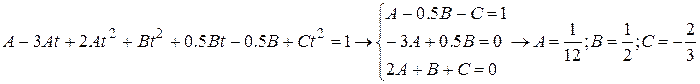
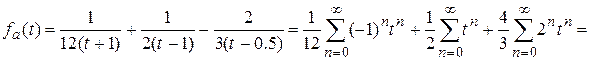
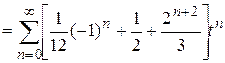 .
.
Отсюда 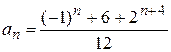 .
.
Определение. Функцией Эйлера называется функция 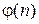 , определенная на множестве N, значения которой равны числу k натуральных, может быть, и составных целых чисел, взаимно простых с n и не превосходящих n, т.е.
, определенная на множестве N, значения которой равны числу k натуральных, может быть, и составных целых чисел, взаимно простых с n и не превосходящих n, т.е.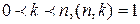 .
.
Для n=1 полагают 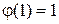 . Знаком
. Знаком 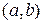 обозначается наибольший общий делитель натуральных чисел a и b. Взаимно простыми называются числа, наибольший делитель которых равен единице. Например, натуральные числа 5 и 7 взаимно просты, т.к. (5,7)=1.
обозначается наибольший общий делитель натуральных чисел a и b. Взаимно простыми называются числа, наибольший делитель которых равен единице. Например, натуральные числа 5 и 7 взаимно просты, т.к. (5,7)=1.
Функция Эйлера аналитически выражается следующим образом:
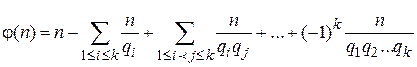 , (1)
, (1)
где к – есть число простых делителей qi числа n, i=1;2;…;k.
Чаще функция Эйлера записывается в другом виде
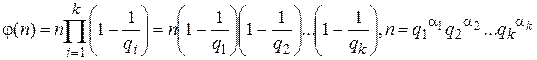 . (2)
. (2)
Посчитаем значения 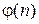 для n=1;2;…;10. Разложим в таблице1 числа с 1 до 10 на простые делители.
для n=1;2;…;10. Разложим в таблице1 числа с 1 до 10 на простые делители.
Таблица 1
| 1=11 | 6=2131 |
| 2=21 | 7=71 |
| 3=31 | 8=23 |
| 4=22 | 9=32 |
| 5=51 | 10=2151 |
1. 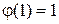 по определению.
по определению.
2. 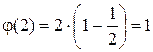 , (1,2)=1. Это число1.
, (1,2)=1. Это число1.
3. 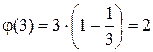 , (1,3)=1; (2,3)=1. Два числа не превосходят 3 и взаимно просты с числом 3; это числа 1 и 2.
, (1,3)=1; (2,3)=1. Два числа не превосходят 3 и взаимно просты с числом 3; это числа 1 и 2.
4. 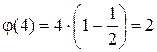 , (1,4)=1; (3,4)=1. Это числа 1 и 3.
, (1,4)=1; (3,4)=1. Это числа 1 и 3.
5. 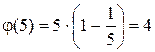 , (1,5)=1; (2,5)=1; (3,5)=1; (4,5)=1. Четыре числа удовлетворяют условию существования функции Эйлера. Это числа 1,2,3,4.
, (1,5)=1; (2,5)=1; (3,5)=1; (4,5)=1. Четыре числа удовлетворяют условию существования функции Эйлера. Это числа 1,2,3,4.
6. 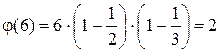 , (1,6)=1; (5,6)=1. то числа 1 и 5.
, (1,6)=1; (5,6)=1. то числа 1 и 5.
7. 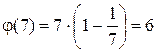 , (1,7)=1; (2,7)=1; (3,7)=1; (4,7)=1; (5,7)=1; (6,7)=1. Значения функции Эйлера в этом случае равно шести, т.к. шесть чисел удовлетворяют условию существования функции Эйлера. Это числа 1,2,3,4,5,6.
, (1,7)=1; (2,7)=1; (3,7)=1; (4,7)=1; (5,7)=1; (6,7)=1. Значения функции Эйлера в этом случае равно шести, т.к. шесть чисел удовлетворяют условию существования функции Эйлера. Это числа 1,2,3,4,5,6.
8. 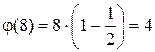 , (1,8)=1; (3,8)=1; (5,8)=1; (7,8)=1. Значение функции Эйлера равно четырем. Это числа 1,3,5,7.
, (1,8)=1; (3,8)=1; (5,8)=1; (7,8)=1. Значение функции Эйлера равно четырем. Это числа 1,3,5,7.
9. 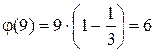 , (1,9)=1; (2,9)=1; (4,9)=1; (5,9)=1; (7,9)=1; (8,9)=1. Это числа 1,2,4,5,7,8.
, (1,9)=1; (2,9)=1; (4,9)=1; (5,9)=1; (7,9)=1; (8,9)=1. Это числа 1,2,4,5,7,8.
10. 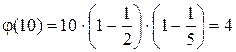 , (1,10)=1; (3,10)=1; (7,10)=1; (9,10)=1. Это числа 1,3,7,9.
, (1,10)=1; (3,10)=1; (7,10)=1; (9,10)=1. Это числа 1,3,7,9.
Функция Эйлера для первых десяти значений аргумента может быть задана как в табл.2.
Таблица 2
| n | ||||||||||
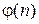 |
Свойства функции Эйлера:
1. Если 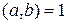 , то
, то 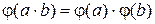 .
.
Пример. (3,7)=1, то 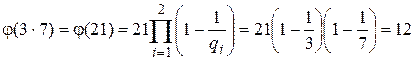 ,
,
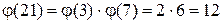 .
.
2. 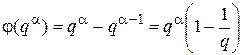 .
.
Пример. Возьмем n=8; n=23,
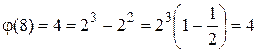 .
.
3. 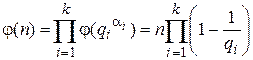 .
.
4. 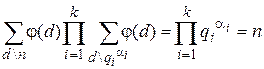 , где d – различные делители числа n.
, где d – различные делители числа n.
Пример. Если n=10=2151, то 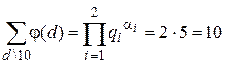 .
.
Выражение 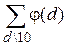 означает, что суммирование ведется по всем делителям числа10
означает, что суммирование ведется по всем делителям числа10
т.е. 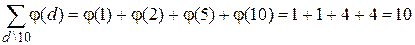 .
.
5. 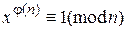 , где
, где 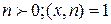
Пример. x=3; x=7.
Решение. 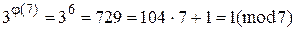
Или 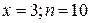 , то
, то 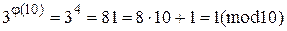 .
.
 2014-02-09
2014-02-09 3455
3455