При подключении ее к источнику ЭДС

Расчет отраженных волн в линии с распределенными параметрами

После того как падающие волны 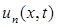и 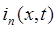достигнут конца линии, при 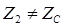возникнут отраженные волны и законы распределения напряжения и тока вдоль линии будут определяться наложением этих волн:

,

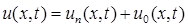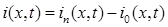
Рассмотрим режим конца линии после прохождения падающей волны. Будем считать, что формы падающих волн 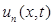и 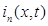нам известны. Тогда получим:

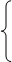
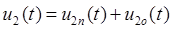(1)

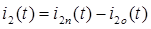(2)

Умножим члены второго уравнения на 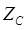и почленно сложим левые и правые части уравнений:

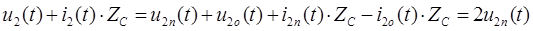
Полученному уравнению соответствует расчетная схема замещения для конца линии (рис. 189).

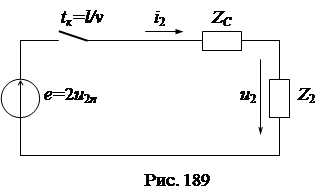В расчетной схеме ЭДС равна 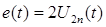, линия представлена своим волновым со­противлением 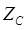, а нагрузка – своими физическими параметрами R, L, C. Момент коммута­ции в расчетной схеме должен происходить с задерж­кой времени 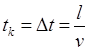, равный времени прохождения линии падающей вол­ной.

Таким образом, для определения напряжения и тока в конце лини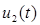и и 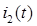с уче­том наложения падающей и отраженной волн, необходимо выполнить расчет переходного процесса в схеме замещения для конца линии и определить искомые величины.

Ранее при решении дифференциальных уравнений линии были получены выражения в общем виде для отраженных волн:

;

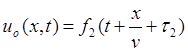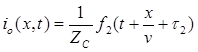
Чтобы достичь начала линии (х = 0) отраженной волне потребуется время 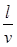, а с мо­мента включения линии пройдет время 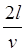и, следовательно, 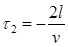. Таким образом:

; .

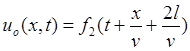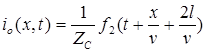Заменим в выражениях для отраженных волн переменную x на y из усло­вия x = l-y:

; .

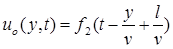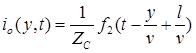Выражения для отраженных волн в конце линии могут быть получены из найденных ранее решений для напряжения и тока в конце линии , :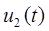

, .

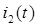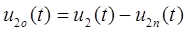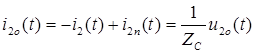Выражения для законов распределения отраженных волн вдоль линии по­лучим из уравнений этих волн в конце линии путем замены в них переменной t на .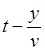

Рассмотрим примеры расчета отраженных волн в линии.

Пример 1. В момент t = 0 линия с волновым сопротивлением 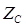вклю­чается к ис­точ­нику постоянной ЭДС e (t) =E, .

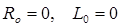Падающие волны будут иметь прямоугольный фронт: ; .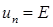

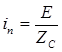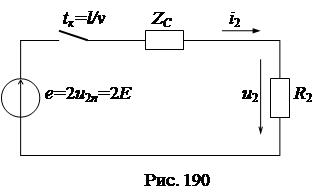
Напряжение и ток в конце линии находим из расчета схемы замещения для конца ли­нии (рис.6). Так как в этой схеме содержаться только активные элементы, то режим в схеме установится мгновенно без переходного процесса:

; .

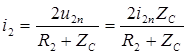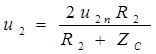Отраженные волны в конце линии:

.

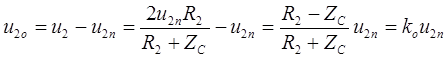
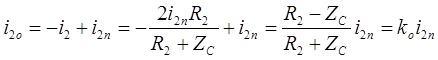Здесь 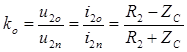- коэффициент отраженной волны.

В случае активной нагрузки отраженные волны в линии можно опреде­лять через ко­эффициент отражения:

, .

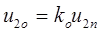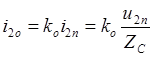Сопротивление нагрузки 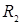может изменяться от 0 до 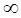. В режиме холо­стого хода 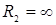, следовательно, коэффициент отраженной волны 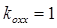. В режиме согласованной нагрузк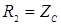и и 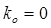, в режиме короткого замыка­ния 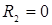и 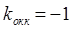. Это означает, что в режиме холостого хода падающие волны полностью отражаются от конца линии с тем же знаком, в режиме корот­кого замыкания – с противоположным знаком, а при согласован­ной нагрузке отраженные волны вообще отсутствуют.

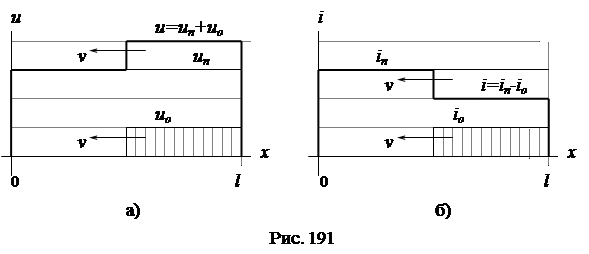
Пусть 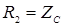, тогда 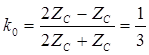и 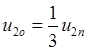, 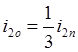. Графи­ческие диа­граммы распределения напряжения и тока вдоль линии с учетом от­раженных волн показаны на рис. 191а, б.

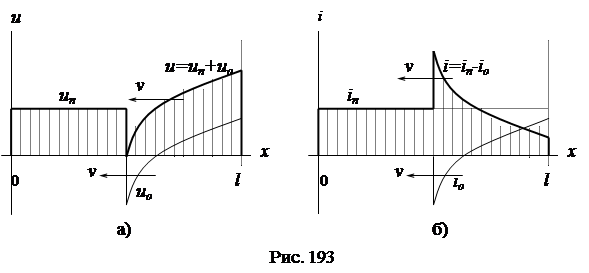
Пример 2. В момент t = 0 линия с волновым сопротивлением 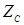вклю­чается к ис­точнику постоянной ЭДС e (t) = E, 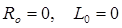. В конце линии включен конденсатор С.

Падающие волны будут иметь прямоугольный фронт: ; .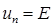

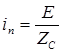Напряжение и ток в конце линии находим из расчета переходного про­цесса в схеме замещения для конца линии (рис. 192).

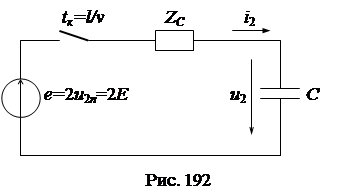Рассчитываем переходной процесс в схеме классическим методом и полу­чаем:

; ,

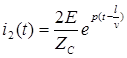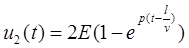где 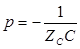- корень характеристического уравнения, переменная t заменена на 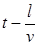с учетом смещения начала переходного процесса в конце линии на .

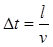Отраженные волны напряжения и тока в конце линии:

.

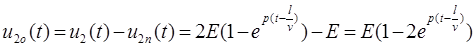
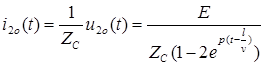Выражения для распределения отраженных волн вдоль линии получим из их выраже­ний для конца линии путем замены переменной t на :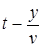

, .

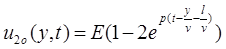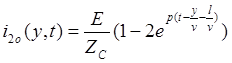Графические диаграммы распределения напряжения и тока вдоль линии с учетом от­раженных волн показаны на рис. 193а, б.