Отражений волн

Расчет переходного процесса в линии с учетом многократных

Переходной процесс в линии с распределенными параметрами складыва­ется из нало­жения волн после их многократных отражений не только от конца линии, но и от ее начала, если внутреннее сопротивление источника не равно волновому сопротивлению линии .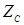

Рассмотрим протекание переходного процесса в идеальной линии без по­терь с волно­вым сопротивлением 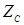в режиме холостого хода (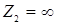) при включении ее к идеальному источнику постоянной ЭДС e (t) =E, .

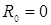Для расчета отраженных волн будем пользоваться коэффициентом отра­жения, кото­рый равен для конца линии 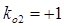и для начала линии .

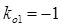Весь переходной процесс состоит из 4-х отрезков времени или стадий.

1-ая стадия. В момент t =0 линия включается к источнику ЭДС e (t) =E и возникают первые (по порядку) падающие волны с прямоугольным фронтом 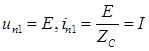, кото­рые перемещаются от начала линии к ее концу с фазо­вой скоростью v (рис. 194а.).

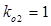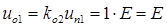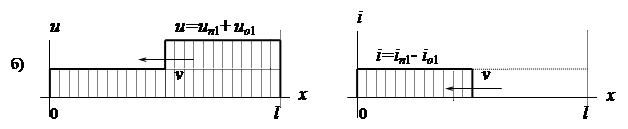
2-ая стадия. Падающие волны, достигнув конца линии, отражаются с ко­эффициент­ом , т.е. , 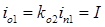. Напряжение и ток вдоль линии оп­ределя­ются как результат наложения падающих и отраженных волн:

, .

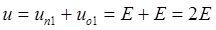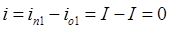Диаграммы функций u(x), i(x) показаны на рис. 194б.

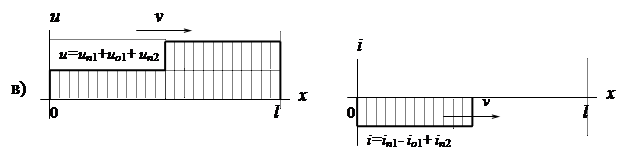
3-я стадия. 1-е отраженные волны достигают начала линии и отражаются с коэффи­ци­ентом 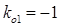, т.е. с обратным знаком, в результате этого отраже­ния появляются 2-е (по по­рядку) падающие волны: , .

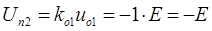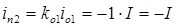Напряжение и ток вдоль линии определяются как результат наложения двух падаю­щих и од­ной отражённой волн:

, .

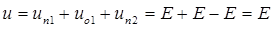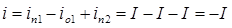Диаграммы функций u(x), i(x) показаны на рис. 10 в.

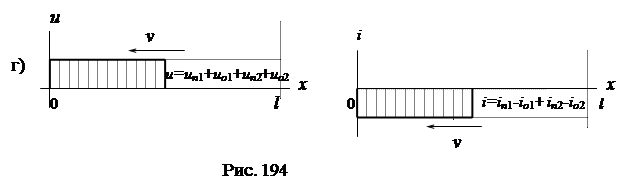
4-ая стадия. 2-е падающие волны, достигнув конца линии, отражаются с коэффици­ентом 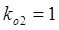, в результате этого отражения появляются 2-ые (по по­рядку) отраженные волны: т.е. 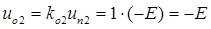, 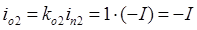. Напряжение и ток вдоль ли­нии определяются как ре­зультат наложения падающих и отраженных волн:

, .

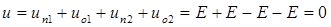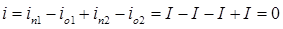Диаграммы функций u(x), i(x) показаны на рис. 10 г. В конце 4-ой стадии напряжение и ток в линии становятся равными нулю, после чего процесс в ли­нии повторяется по тому же сценарию. Период повторения .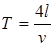

В реальных линиях наличие потерь (хоть и незначительных) приводит к быстрому затуханию переходного процесса.

Если в линии содержатся только активные элементы, то расчет переход­ного процесса и построение графических диаграмм распределения и напряже­ния и тока вдоль линии при многократных отражениях волн выполняются по тому же алгоритму, как и для рассмотрен­ного выше случая холостого хода, c той лишь разницей, что коэффициенты отражения в на­чале и конце линии опре­деляются по формуле 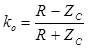и могут иметь любые значения в интервале от –1 до +1.

Если линия содержит накопители энергии L или C, то после отражения волн от этих элементов изменяются формы волн. Расчет каждой новой отра­женной волны становится все сложнее, в результате чего расчет переходного процесса по методу наложения волн стано­вится практически невозможным. В этом случае применяются специальные методы расчета, рассмотрение которых выходит за рамки учебного курса ТОЭ.

Часть 2. Теория нелинейных цепей