2014-02-09
567
Как уже отмечалось ранее, источник неограниченной мощности чаще всего используется на стадии “загонки” примеси. Для вычисления количества примеси в этом случае достаточно проинтегрировать (3.24) по всему пространству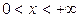 
. Формальное вычисление этого интеграла оказывается достаточно длительным. Проще сначала вычислить зависящую от времени величину потока примеси через поверхность 
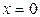, и затем проинтегрировать по всему времени “загонки”.
Исходя из (3.4) и (3.5):
; 
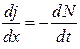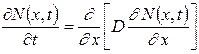
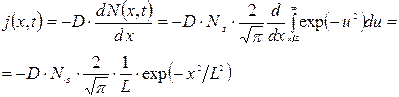(3.25)
Соответственно,
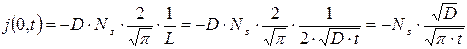(3.26)
После интегрирования абсолютной величины потока примеси по t получим:
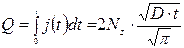(3.27)
3.3.2. Диффузия из слоя конечной толщины
Много важных для практики решений уравнения диффузии могут быть получены с использованием принципа суперпозиции решений линейного уравнения диффузии с линейными же начальными условиями.
Допустим, в толще бесконечно толстой пластины расположен однородно легированный слой толщиной 2h с концентрацией примеси No (рис.3.4).
Примем, что x=0 находится в середине этого слоя. Такой профиль распределения примеси может быть представлен в виде суперпозиции двух профилей, для одного из которых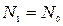 
для всех 
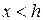, и не содержащем примеси во всей остальной области. Для второго профиля условие 
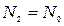выполняется в области 
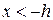, а остальная область также не легирована. Обе области, таким образом, относятся к уже рассмотренному случаю диффузии примеси из одной полуограниченной области в другую.
Решения для них записываются в виде:
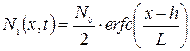и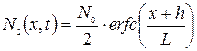 
(3.28)
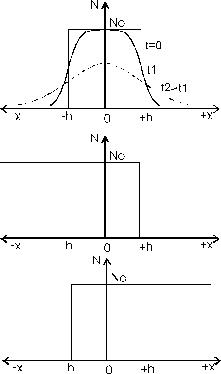
Исходный профиль по принципу суперпозиции получается как разность N1–N2, т.е.
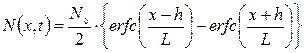(3.28)
Заметим, что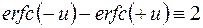 
3.3.3. Диффузия из бесконечно тонкого слоя (точечный источник)
От (3.28) легко перейти к случаю диффузии из бесконечно тонкого слоя (из точечного источника). Запишем erfc -функции в виде определяющих их интегралов:
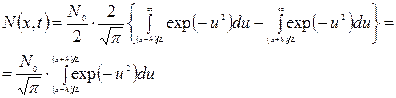(3.29)
При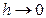 
интеграл стремится к 
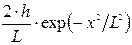и если принять, что 
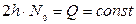, а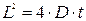 
выражение для N(x,t) примет вид:
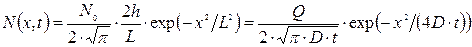.(3.29)
совпадающий с (3.10б) – Гауссово распределение примеси (рис. 3.5).
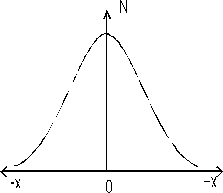
Понятие тонкого и толстого слоя.
Если h>4L – слой толстый, если h < L/ 4 – слой тонкий, вычисления по (3.27) будут численно совпадать с получаемыми по формуле (3.29). Это будет случай тонкого слоя.
