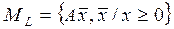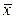Модель МОБ как частный случай модели Неймана

,

- вектор интенс-ти,А-матрица затрат, В-матрица выпуска(единичная).

Доказывается, что м построить сбаланс-ую траекторию, темп роста этой траектории:

,

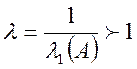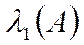-max по модулю собс-ое число матрицы А.

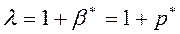-темп роста цен.

Магистральная модель накопления.

Сильная теорема о магистрали. Задана целевая функция, кот оценивает полез-ть рез-ов пр-ва(линейная).

.

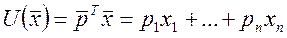Ее нужно макс-ть на отрезке [0,T]. На каждом шаге продукты на этом периоде явл ресурсами на след-й период. Суть: оптим-ая траектория только в начале и в конце пути м отличатся от магистрали, в остальном она совпадает с магистралью.

Магистральная модель накопления. Вэтой модели учит-ся процесс накопления, т.е. расширение ОФ. Вводятся понятия:

Конечный продукт=потребление+накопление.

Задается матрица прямых затрат (Леонтьева), матрица кап-ых затрат. Составл-ся ур-ние потребления, с помощью опред-ых преобр-ий строится магистраль. Заданы след-щие параметры:

, ,

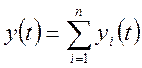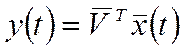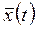-вектор валовых выпусков, 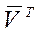-вектор добав-ых стоим-ей на единицу вал-ой продукции. Конечная продукция = добав-ой стоим-ти.

,

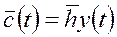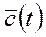-вектор потребления, -вектор показывает как распр-ся конечный продукт по различным напр-иям потребления, задает стр-ру потребл-ия конечного продукта ,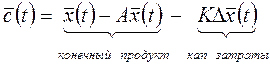

К- матрица кап затрат,

А-матрица прямых затрат,

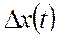-припост продукта, кот д б обеспечен за счет инвестиций.

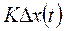-сколько продукта всех отраслей необходимо для увел-ния выпуска.

.

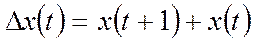
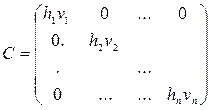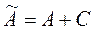-объем промеж-го и личного потребл-ия,

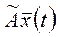-вектор промеж-ых продуктов и личного потребления.

.

.

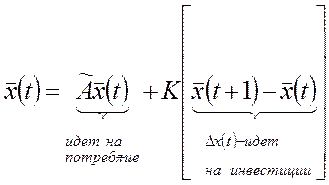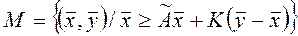y -выпуск в след-ем периоде, х –выпуск в данном периоде, М-технол-ое мн-во. На нем строится магистраль.

-невырожденная матрица. 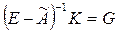. Если G, то сущ-т магистраль. При этом 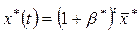, 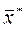-начальный вектор, 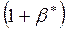-темп роста выпуска, 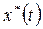-собст-ый вектор матрицы G, кот соотв-т max по модулю собст-му числу 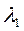матрицы G. 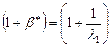. Позволяет найти соотн-ие потребления и накопления.